僈僂僗娭悢偵帡偨娭悢丂update 20181104
僈僂僗娭悢偲偼
庴尡惗偵偲偭偰曃嵎抣偲偄偆扨岅偼偁傑傝嬁偒偺椙偄傕偺偱偼側偄偱偟傚偆丅偙偺曃嵎抣偺傕偲偵側偭偰偄傞偺偑摑寁偺昗弨曃嵎偺峫偊曽偱偡丅屄乆偵偼屄惈偑偁傞偑丄偨偔偝傫廤傑傟偽偦偺廤抍偺摿挜偑尒偊偰偔傞丄偲偄偆傕偺偱偡丅
摿挜傪偁傜傢偡傕偺偲偟偰丄暯嬒偲偦偙偐傜偺偽傜偮偒嬶崌偑偁傝傑偡丅
摑寁偱偼丄偄傠偄傠側宍偺暘晍偑偱偰偒傑偡偑丄戙昞揑側宍偑僈僂僗暘晍偱偡丅僈僂僗暘晍偼丄師偱帵偡僈僂僗娭悢偱昞偡偙偲偑偱偒傑偡丅
y亖exp(-x^2)丂丒丒丒嘆
偙傟偼丄忋偵撌偺扨曯惈偺娭悢偱偡丅
偙偺娭悢偼巊偄彑庤偑椙偄偺偱摑寁偺暘栰偩偗偱偼側偔丄偄傠偄傠側応柺偱巊傢傟偰偄傑偡丅偦偺偲偒偼丄堦斒揑側娭悢偺宍偵偟偰巊偄傑偡丅
y亖d+c*exp(-1*(b*(x-a))^2)丂丒丒丒嘇
學悢a丄d偼x幉丄y幉曽岦傊偺暯峴堏摦偺戝偒偝丄學悢b丄c偱x幉丄y幉曽岦傊偺怢弅偺戝偒偝傪昞偟丄偄偢傟傕0埲忋偺幚悢偱偡丅
a亖0丄b亖1丄c亖1丄d亖0丄偲偍偔偲嘆幃偵側傝傑偡丅
恾偵昤偔偲師偺僌儔僼偵側傝傑偡丅
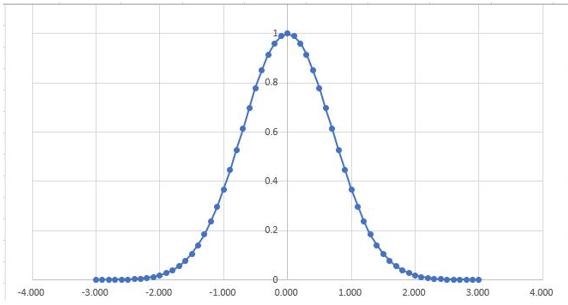
倷亖exp(-x^2)
y亖1/(1+x^2)
師偵僈僂僗娭悢偺傛偆偵忋偵撌偺扨曯惈偺娭悢偲偟偰
y亖1/(1+x^2)丂丒丒丒嘊
偑峫偊傜傟傑偡丅
偙偙偱嘆幃偲嘊幃傪尒偰丄偙傟傜偺娭悢偑偳傟傎偳帡偰偄傞偺偐丄偁傞偄偼帡偰偄側偄偺偐傪敾抐偟偰傒傑偟傚偆丅
斾妑偡傞娭悢偼丄
y亖d+c*exp(-1*(b*(x-a))^2)丂丒丒丒嘇
側偺偱丄偙偺學悢傪巊偭偰嘊幃傪堦斒偺宍幃偵偡傞偲丄
y亖d+c/(1+(k*(b*(x-a))^2)丂丒丒丒嘋
偲偄偆宍偵側傝傑偡丅a乣d傑偱偑嫟捠偺學悢偱丄k偺曄壔偱僈僂僗娭悢偵懳偟偰斾妑偡傞娭悢偺峀偑傝嬶崌傪挷惍偟傑偡丅娭悢憡屳偺帡偰偄傞娭學傪悢帤偱昞偡偲偒丄偙偺悢帤偺偙偲傪壖偵憡娭學悢偲屇傇偙偲偲偟傑偡丅
偪側傒偵丄a亖0丄b亖1丄c亖1丄d亖0偲偟丄k亖e亅1乮e丗僱僀僺傾悢乯偲偡傞偲丄嘇幃媦傃嘋幃偼丄x亖亇1偱y亖1/e丂偵側傝傑偡丅
2偮偺娭悢傪斾妑偡傞曽朄偺堦偮偵憡屳憡娭娭悢偑偁傝傑偡丅
堦斒揑側娭悢f(x)偲g(x)偺憡屳憡娭娭悢冇fg(冄)偼丄
冇fg (冄)亖 lim (1/(2*x))佺丂f(x)*g(x+冄)dx
偙偙偱lim乮嬌尷乯偼亂x 仺 亣亃偱偁傝丄佺(愊暘)偺斖埻偼亂-x 仺 x亃偱偡丅
棧嶶揑昞尰偺愊榓憡屳憡娭娭悢偼
冇fg (冄)亖(1/n)嚁f(xi)*g(xi+冄)
偙偙偱嚁乮愊榓乯偺斖埻偼亂i=1 仺 値亃偱偡丅
憡娭娭悢偺宍偼偳偆偁傟丄婯奿壔偝傟偨嵟戝抣偺悢抣偑拝栚揰偱偡丅
娭悢偺帺暘帺恎偺憡娭偼帺屓憡娭娭悢偲偄偄傑偡偑丄婯奿壔偝傟偨帺屓憡娭娭悢偺嵟戝抣偼偳偺娭悢傪偲偭偰傕1偵側傝傑偡丅
偮傑傝丄婯奿壔偝傟偨憡娭娭悢偺嵟戝抣偑1偵偳傟偩偗嬤偄偐偱娭悢偑帡偰偄傞偙偲傪昞尰偱偒傞偲偟傑偡丅偡側傢偪丄
嵟戝抣偱偺婯奿壔憡娭學悢偼丂s亖 冇fg (0)/(sqrt(冇ff (0)乯*sqrt(冇gg (0)))
偲側傝傑偡丅
冇fg (0)偲彂偗傞偺偼丄嘇幃傕嘋幃傕x亖0偱嵟戝抣偺嬼娭悢偩偐傜丄憡屳憡娭娭悢偑冄亖0偱嵟戝抣傪帵偡偐傜偱偡丅
偦傟偱偼丄
f(x)亖exp(-x^2)丄
g(x)亖1/(1+(k*x^2))
偲偍偄偰丄x1亖-3.0丄x2亖-2.9丄丒丒丒丄x60亖2.9丄x61亖3.0丄偺娫偺憡娭學悢s傪愊榓寁嶼偟傑偡丅
k傪曄壔偝偣偰s偺摦偒傪尒傞偲
k=1.00丄 s亖0.9637638900
k=1.25丄 s亖0.9750893706
k=1.50丄 s亖0.9818002228
k=e-1丄 s亖0.9852351488
k=1.75丄 s亖0.9855932236
k=2.00丄 s亖0.9874479508
k=2.2485丄s亖0.9879686321
k=2.2490丄s亖0.9879686352
k=2.2495丄s亖0.9879686346
k=2.25丄 s亖0.9879686303
k=2.50丄 s亖0.9875169655
k=3.00丄 s亖0.9848519010
k=2.2490偺廃曈偵s偺嵟戝抣偑偁傝偦偆偱偡丅
崱丄2師嬋慄s=a*k^2+b*k+c偲偍偄偰嵟戝抣偲偦偺埵抲傪媮傔偰傒傑偡丅
k1=2.2485丄s1=0.9879686321
k2=2.2490丄s2=0.9879686352
k3=2.2495丄s3=0.9879686346
傪巊偭偰楢棫堦師曽掱幃傪師偺傛偆偵棫偰傑偡丅
0.9879686321=a*(2.2485)^2+b*(2.2485)+c
0.9879686352=a*(2.2490)^2+b*(2.2490)+c
0.9879686346=a*(2.2495)^2+b*(2.2495)+c
偙傟傪夝偄偰丄a丄b丄c偼埲壓偺傛偆偵側傝傑偡丅
a= -0.0074000001
b= 0.0332877005
c= 0.9505338048
嵟戝抣偺k嵗昗偼k=-b/(2*a)
亪丂k= 2.2491689188
偦偺帪偺嵟戝抣偼s=a*k^2+b*k+c
亪丂s= 0.9879686354
偙偺帪偺娭悢偺宍偼師偺僌儔僼偺傛偆偵側傝傑偡丅x亖1.2晅嬤偱僈僂僗娭悢偲岎嵎偟傑偡丅
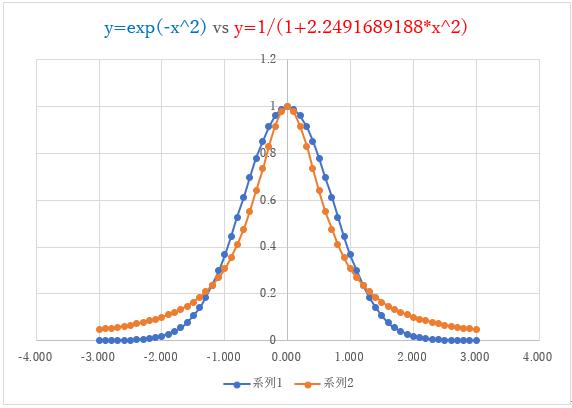
2師嬋慄
僈僂僗娭悢偵帡偨娭悢偺椺偑堦偮偩偗偱偡偲怱傕偲側偄偺偱偡偑丄巆擮側偑傜弨旛偱偒偰偄傞偺偼偙偺娭悢偺傒偱偡丅
忋偵撌偺2師嬋慄傕岓曗偵嫇偑傝傑偡偑丄x傪曄壔偝偣傞偲偒偵y亞0偺斖埻傪偄偪偄偪峫椂偟側偄偲偄偗側偄偨傔丄僈僂僗嬋慄偲斾傋傞偵偼擄偑偁傝傑偡丅
偟偐偟丄傗偭偰傒傑偟傚偆丅
嘋幃偺傛偆側宍偵惍偊傞偲丄2師嬋慄偼埲壓偺傛偆偵昞偣傑偡丅
y亖d+c-c*k*((x-a)*b)^2丒丒丒嘍
摨偠傛偆偵丄a亖0丄b亖1丄c亖1丄d亖0偲偟丄k亖1-乮1/e乯乮e丗僱僀僺傾悢乯偺偲偒偵嘍幃偼丄x亖亇1偱y亖1/e丂偵側傝傑偡丅
g(x)亖1-k*x^2丂乮y亞0乯
g(x)亖0丂(y亙0)
偲偟偰-3.0亝x亝3.0偺斖埻偱k傪曄壔偝偣偰愊榓憡屳憡娭娭悢冇fg (冄)傪寁嶼偟丄婯奿壔憡娭娭悢s偺摦偒傪傒偰傒傑偡丅
k=0.20丄 s亖0.9229401295
k=0.30丄 s亖0.9673858325
k=0.40丄 s亖0.9862630203
k=0.45丄 s亖0.9903837742
k=0.50丄 s亖0.9923506371
k=0.525丄s亖0.9926885058
k=0.550丄s亖0.9928081451
k=0.575丄s亖0.9922822059
k=0.60丄 s亖0.9914749649
k=0.70丄 s亖0.9867401283
k=0.550偺廃曈偵s偺嵟戝抣偑偁傝偦偆偱偡丅
崱丄2師嬋慄s=a*k^2+b*k+c偲偍偄偰嵟戝抣偲偦偺埵抲傪媮傔偰傒傑偡丅
k1=0.525丄s1=0.9926885058
k2=0.550丄s2=0.9928081451
k3=0.575丄s3=0.9922822059
傪巊偭偰楢棫堦師曽掱幃傪師偺傛偆偵棫偰傑偡丅
0.9926885058=a*(0.525)^2+b*(0.525)+c
0.9928081451=a*(0.550)^2+b*(0.550)+c
0.9922822059=a*(0.575)^2+b*(0.575)+c
偙傟傪夝偄偰丄a丄b丄c偼埲壓偺傛偆偵側傝傑偡丅
a=-0.0074000001
b= 0.0332877005
c= 0.9505338048
嵟戝抣偺k嵗昗偼k=-b/(2*a)
亪丂k= 0.5421330268
偦偺帪偺嵟戝抣偼s=a*k^2+b*k+c
亪丂s= 0.9928401086
s傪斾妑偡傞偲丄2師嬋慄偺昞尰偺曽偑丄傛傝僈僂僗娭悢偵帡偰偄傞偲偄偆偙偲偵側傝傑偟偨丅暋嶨側怱嫬偱偡丅
偙偺帪偺娭悢偺宍偼師偺僌儔僼偺傛偆偵側傝傑偡丅偙偺娭悢傕x亖1.2晅嬤偱僈僂僗娭悢偲岎嵎偟傑偡丅
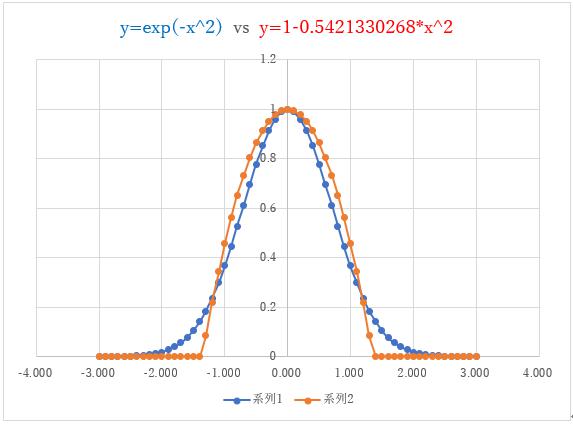
師偼丒丒
偁傞嬋慄偺堦晹傪y亞0媦傃x亖0偱嬼娭悢偲偄偆忦審晅偒偱愗傝庢偭偰偒偰僈僂僗娭悢偵帡偨娭悢偲偟偰埖偆偙偲偼偱偒傑偡丅偟偐偟丄忦審偵婥傪巊偄側偑傜偲偄偆偺偼丄偲偰傕埖偄偯傜偄娭悢偲偄偆偙偲偵側傝傑偡丅
傕偆傂偲偮偐傆偨偮丄忦審傪婥偵偟側偔偰傛偄僈僂僗娭悢偵帡偨扨曯惈偺娭悢傪尒偮偗偰偒偰丄婯奿壔憡娭學悢傪寁嶼偟偰傒偨偄偲巚偭偰偄傑偡丅
----- 偙偙傑偱丂20181104 -----
偍傑偗
偍傑偗偲偟偰丄嶰妏娭悢偺梋尫嬋慄傪巊偭偰
倷亖d+c*(cos(b*k*(x-a)))^2
傪峫偊偰傒傑偡丅偨偩偟丄亅(兾/2)亝b*k*(x-a))亞(兾/2乯偱偡丅
偙偙偱丄a亖0丄b亖1丄c亖1丄d亖0偲偟丄k亖arccos(1/e)偺偲偒丄x亖亇1偱梌幃偼倷亖1/e偵側傝傑偡丅
g(x)亖(cos(k*x))^2
亅(兾/2)亝k*x亞(兾/2乯
偲偟偰-3.0亝x亝3.0偺斖埻偱k傪曄壔偝偣偰愊榓憡屳憡娭娭悢冇fg (冄)傪寁嶼偟丄婯奿壔憡娭娭悢s偺摦偒傪傒偰傒傑偡丅
k=1.000丄s亖0.9939720180
k=0.950丄s亖0.9968806440
k=0.925丄s亖0.9978217530
k=0.900丄s亖0.9983741840
k=0.875丄s亖0.9985044640
k=0.850丄s亖0.9981707070
k=0.800丄s亖0.9959493020
k=0.875偺廃曈偵s偺嵟戝抣偑偁傝偦偆偱偡丅
崱丄2師嬋慄s=a*k^2+b*k+c偲偍偄偰嵟戝抣偲偦偺埵抲傪媮傔偰傒傑偡丅
k1=0.900丄s1=0.9983741840
k2=0.875丄s2=0.9985044640
k3=0.850丄s3=0.9981707070
傪巊偭偰楢棫堦師曽掱幃傪師偺傛偆偵棫偰傑偡丅
0.9983741840=a*(0.900)^2+b*(0.900)+c
0.9985044640=a*(0.875)^2+b*(0.875)+c
0.9981707070=a*(0.850)^2+b*(0.850)+c
偙傟傪夝偄偰丄a丄b丄c偼埲壓偺傛偆偵側傝傑偡丅
a=-0.3712296000
b= 0.6537213400
c= 0.7107209540
嵟戝抣偺k嵗昗偼k=-b/(2*a)
亪丂k= 0.8804811631
偦偺帪偺嵟戝抣偼s=a*k^2+b*k+c
亪丂s= 0.9985156169
s傪斾妑偡傞偲丄梋尫嬋慄偺昞尰偺曽偑丄2師嬋慄偺昞尰傛傝傕丄偝傜偵僈僂僗娭悢偵帡偰偄傞偲偄偆偙偲偵側傝傑偟偨丅偝傜偵偝傜偵暋嶨側怱嫬偱偡丅
偙偺帪偺娭悢偺宍偼師偺僌儔僼偺傛偆偵側傝傑偡丅偙偺娭悢傕x亖1.2晅嬤偱僈僂僗娭悢偲岎嵎偟傑偡丅
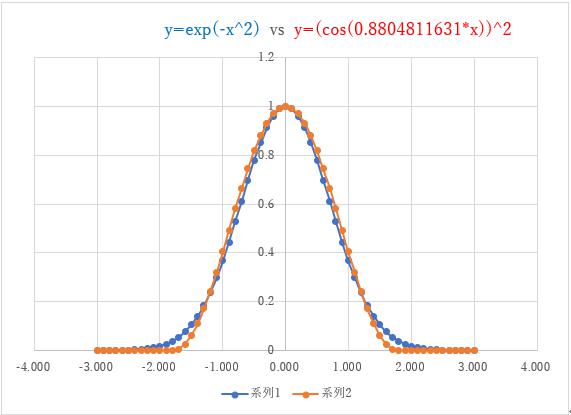
(偍傑偗)丱2
乮偍傑偗)^2偲偟偰丄扨敪偺嶰妏攇傪巊偭偰
倷亖d+c*(-1*k*b*abs(x-a)+1)
傪峫偊偰傒傑偡丅
偙偙偱丄a亖0丄b亖1丄c亖1丄d亖0偲偟丄k亖(e-1)/e偺偲偒丄x亖亇1偱梌幃偼丂倷亖1/e偵側傝傑偡丅
g(x)亖-k*abs(x)+1
丂乮偨偩偟丂g(x)<0丂偺偲偒丂g(x)=0乯
偲偟偰-3.0亝x亝3.0偺斖埻偱k傪曄壔偝偣偰愊榓憡屳憡娭娭悢冇fg (冄)傪寁嶼偟丄婯奿壔憡娭娭悢s偺摦偒傪傒偰傒傑偡丅
k=0.50丄s亖0.9850231022
k=0.55丄s亖0.9935982368
k=0.60丄s亖0.9974543052
k=0.65丄s亖0.9974779310
k=0.70丄s亖0.9944148687
k=0.75丄s亖0.9890006580
k=0.65偺廃曈偵s偺嵟戝抣偑偁傝偦偆偱偡丅
崱丄2師嬋慄s=a*k^2+b*k+c偲偍偄偰嵟戝抣偲偦偺埵抲傪媮傔偰傒傑偡丅
k1=0.60丄s1=0.9974543052
k2=0.65丄s2=0.9974779310
k3=0.70丄s3=0.9944148687
傪巊偭偰楢棫堦師曽掱幃傪師偺傛偆偵棫偰傑偡丅
0.9974543052=a*(0.60)^2+b*(0.60)+c
0.9974779310=a*(0.65)^2+b*(0.65)+c
0.9944148687=a*(0.70)^2+b*(0.70)+c
偙傟傪夝偄偰丄a丄b丄c偼埲壓偺傛偆偵側傝傑偡丅
a=-0.6173376200
b= 0.7721445410
c= 0.7564091238
嵟戝抣偺k嵗昗偼k=-b/(2*a)
亪丂k= 0.6253827047
偦偺帪偺嵟戝抣偼s=a*k^2+b*k+c
亪丂s= 0.9978520445
s傪斾妑偡傞偲丄扨敪偺嶰妏攇偺昞尰偺曽偑丄2師嬋慄偺昞尰傛傝傕丄偝傜偵僈僂僗娭悢偵帡偰偄傞偲偄偆偙偲偵側傝傑偟偨丅偲偰傕偲偰傕暋嶨側怱嫬偱偡丅
偙偺帪偺娭悢偺宍偼師偺僌儔僼偺傛偆偵側傝傑偡丅
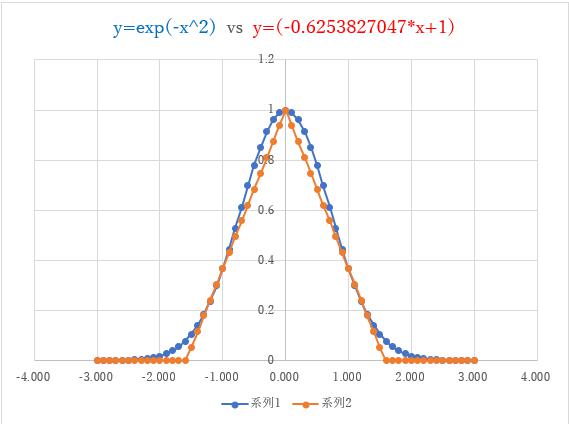
(偍傑偗)丱3
(偍傑偗)^3偲偟偰丄扨敪偺嬮宍攇傪巊偭偰
倷亖1 ,if(abs(x-a) 偙偙偱丄a亖0丄b亖1丂偺偲偒 g(x)亖-k*abs(x)+1 偲偟偰-3.0亝x亝3.0偺斖埻偱k傪曄壔偝偣偰愊榓憡屳憡娭娭悢冇fg (冄)傪寁嶼偟丄婯奿壔憡屳憡娭學悢s偺摦偒傪傒偰傒傑偡丅 k=0.800丄s亖0.9278615780 k=0.95偺廃曈偵s偺嵟戝抣偑偁傝偦偆偱偡丅 k1=0.90丄s1=0.9395205725 0.9395205725=a*(0.90)^2+b*(0.90)+c 偙傟傪夝偄偰丄a丄b丄c偼埲壓偺傛偆偵側傝傑偡丅 嵟戝抣偺k嵗昗偼k=-b/(2*a) 偙偺帪偺娭悢偺宍偼師偺僌儔僼偺傛偆偵側傝傑偡丅 婯奿壔憡屳憡娭學悢s偼丄扨敪偺嬮宍攇偱傕丂0.9435657514丂偲偄偆抣傪帵偟偰偄傑偡丅 ----- 偙偙傑偱丂20181108 -----
丂乮偨偩偟丂g(x)<0丂偺偲偒丂g(x)=0乯
k=0.850丄s亖0.9362820566
k=0.900丄s亖0.9395205725
k=0.950丄s亖0.9432901871
k=1.000丄s亖0.9426415025
k=1.050丄s亖0.9425998825
k=1.100丄s亖0.9425998825
崱丄2師嬋慄s=a*k^2+b*k+c偲偍偄偰嵟戝抣偲偦偺埵抲傪媮傔偰傒傑偡丅
k2=0.95丄s2=0.9432901871
k3=1.00丄s3=0.9426415025
傪巊偭偰楢棫堦師曽掱幃傪師偺傛偆偵棫偰傑偡丅
0.9432901871=a*(0.95)^2+b*(0.95)+c
0.9426415025=a*(1.00)^2+b*(1.00)+c
a=-0.8836598400
b= 1.7101629960
c= 0.1161383465
亪丂k= 0.9676591142
偦偺帪偺嵟戝抣偼s=a*k^2+b*k+c
亪丂s= 0.9435657514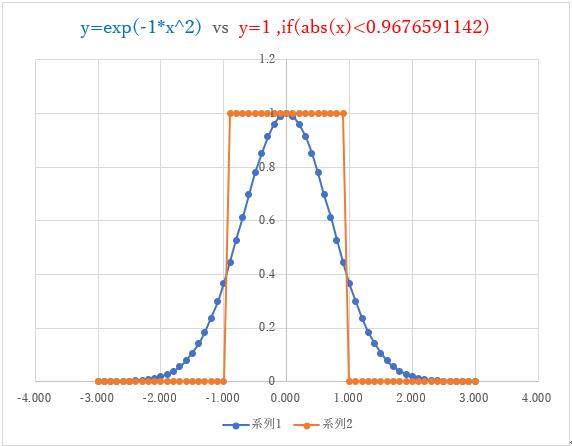
娭悢帺恎偺婯奿壔帺屓憡娭學悢偑1偱偁傞偙偲傪峫偊傞偲丄崱夞寁嶼偟偨5偮偺娭悢偲僈僂僗娭悢偲偺婯奿壔憡屳憡娭學悢s偑0.94埲忋偲偄偆偺偼晄巚媍側婥偑偟傑偡丅
摿偵嬮宍攇偵偮偄偰偼0.6偲偐0.7偲偐偺抣偩傠偆偲峫偊偰偄偨偺偱丄傃偭偔傝偟偰偄傑偡丅