�P�ƂO�@update 20190122
�v�Z�@�̐��E
���𐔂���Ƃ��A���̐l�Ԃ�10�i���Ő����܂��B12�i���Ń_�[�X��O���X�Ő������肷��Ƃ��������܂��B���𐔂���Ƃ�10�i����60�i����g�ݍ��킹�Đ����܂��B
1��0��2��ނ����g��Ȃ�2�i���́A�l�Ԃ̎��Љ�łقƂ�ǎg���Ȃ����ł����A�f�B�W�^���R���s���[�^�̐��E�ł͕K�{�Ȑ��ł��B
1�܂���0�̓�̒l���������ϐ���p����_�����A�u�[���㐔�Ƃ����܂��B�_���㐔�ɂ����邷�ׂẲ��Z�i�_�����Z�j�́A�_���ρi�ȁC�E�CAND�j�A�_���a�i�ɁC�{�COR�j�C�ے�_���i�ʁC^�CNOT�j�̎O�̊�{���Z�̑g�ݍ��킹�ŕ\���ł��A���̘_�����Z�̓I���A�I�t�Ƃ����X�C�b�`�̑g�ݍ��킹�Ŏ����ł��܂��B
���Ȃ킿�A�R���s���[�^�́A�Z�p�v�Z��d�C�I�ȃX�C�b�`�̑g�ݍ��킹�i�_����H�j�ō���Ă���̂ł��B
��1����̃R���s���[�^�͐^��ǂ��X�C�b�`��H�Ƃ��ėp���܂����B���̎��̐���̓g�����W�X�^���X�C�b�`��H�Ƃ��āA���̎��̐���͏W�ω�H�iIC�FIntegrated circuit�j���X�C�b�`��H�Ƃ��āA���̎��̐���͑�K�͏W�ω�H�iLSI�FLarge Scale IC�j���X�C�b�`��H�Ƃ��āA�E�E�E�Ɣ��W���Ă��܂����B
�s�K���Ȑ��E
1��0�̓R���s���[�^�̐��E�̂ق��ɕʂ̐��E�������Ă��܂��B
����́A1��0�݂̂̐���ō����^���s�K���M����^�������̐��E�ŁA�v����Ȋw�V�~�����[�V�����Ŏg�p����Ă��܂��B���̐���̂ЂƂɍő������isquence of maximal period�j�F�l�n����܂��B
�l�n��́A�R���s���[�^�[�v���O�����Ń\�t�g�E�F�A�Ƃ��č��o����ق��ɁA�V�t�g���W�X�^�Ɣr���I�_���a�iEX-OR�j�̑g�ݍ��킹�Ńn�[�h�E�F�A�Ƃ��Ă����o���܂��B
�l�n��Ƃ́H
���K���A��GF(q)���n�������� f(x)�����n�I�iprimitive�j�ł���Ƃ��A�ő����q^n-1���������f(x)�ɂ�萶���ł��܂��B���̌��n�������Ő�������鐔�ő������isquence of maximal period�j���`������̂ł����Aq��2�̂Ƃ��̍ő��������l�n��ƌĂ�ł��܂��B
�K���A�̂Ƃ́H
�����@�i+�j�A���@�i-�j�A��@�i�~�j�A���@�i���j�Ɋւ��āA���Ă���W���i��������0�������j���u�́ifield�j�v�Ƃ����A�L������Ȃ�̂�L���̂܂��̓K���A�́iGalois field�j�Ƃ����܂��Bq�̗v�f����Ȃ�L���̂�GF(q)�ŕ\���܂��Bq=2�̂Ƃ��AGF(2)�ƕ\�L����A�v�f{1,0}���ΏۂƂȂ�܂��B
GF(2)�Ƃ́H
��{0,1} �Ƃ����C�v�f����2�̗L���W�����l���܂��B�����āC�l�����Z���u�����̐��E�Ŏl�����Z�����āC����� 2 �Ŋ������]��v�ƒ�`���܂��B�Ⴆ�C1+1=0�C1�~0=0�C0-1=1�Ƃ��������ł��B
���̒�`�͎l�����Z���������ׂ������i�̂̌����j�����Ă���̂ŁC�L���̂ɂȂ��Ă��܂��B
�����������n�I�ł���Ƃ́H
���^����ꂽ�������̂��ׂĂ̌W���̍ő���̂��Ƃ��u���e�v�Ƃ����̂ł����A���̓��e���u1�v�ɓ��������Ƃł��B���̂Ƃ��̑��������u���n�������v�ł���Ƃ����܂��B���Ȃ킿�A�^����ꂽ�������̊e���̌W����1��0�Ƃ������Ƃł��B
�r���I�_���a�Ƃ́H
��2�̓��͂̂ǂ��炩�Е����^�ł����Е����U�̎��ɂ͌��ʂ��^�ƂȂ�A�����Ƃ��^���邢�͗����Ƃ��U�̎��͋U�ƂȂ鉉�Z�i�_�����Z�j�̂��Ƃł��B
�V�t�g���W�X�^�Ƃ́H
�������̃t���b�v�t���b�v��H���J�X�P�[�h�ڑ������f�W�^����H�̂��Ƃł��B�f�[�^�i1�܂���0�j�����̉�H���ړ�(�V�t�g)���Ă����悤�\������Ă��܂��B
�t���b�v�t���b�v��H�Ƃ́H
���f�B�W�^����H�̈��ŁA�u0�v�܂��́u1�v�̒l��ێ����邱�Ƃ��ł����H�̂��Ƃł��B
�J�X�P�[�h�ڑ��Ƃ́H
�������̉�H�f�q�Ȃǂ��c���ɂȂ����Ƃ������܂��B����ڑ��B
�y�藝�z�`�`�`�`�`�`�`�`�`�`
��f(x)��GF(2)��̑�����
�@�@f(x)=f[0]+f[1]x+f[2]x^2+�E�E�E+f[m]x^m
�@�if[0]=f[m]=1�A[�E]�͓Y������\���܂��j
�ŁA���̎�����m�Ƃ���B
f(x)�͑�����x^(2^m-1)-1������邪�At��2^m-1�ɑ��Af(x)�͑�����x^t-1�������Ȃ��Ƃ���B
���̂Ƃ��A���ׂĂ�s��S[f(x)]�@(�������As=(0,0,0,�E�E�E�E,0)�͏����j
�ɂ��āi���̎����jP(s)=2^m-1�ł���B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`
��̒藝����̓I�Ȑ��������āA�l���Ă݂܂��B
f(x)��GF(2)��̑�����
�@�@f(x)=1+1�x+0�x^2+0�x^3+1�x^4
�@�@�@������m=4�ŁAf[0]=1�Af[1]=1�Af[2]=0�Af[3]=0�Af[4]=1�ł���Ƃ�
f(x)�͑�����x^(2^4-1)-1=x^(16-1)-1=x^15-1������邪�A
������x^14-1�Ax^13-1�A�E�E�Ex^5-1�Ax^4-1�������Ȃ��A
�Ƃ́A
x^15-1�����������imod2�j�����Ƃ��A����f(x)=1+x+x^4�����A�Ƃ������ƁB
�܂��A������x^14-1�Ax^13-1�A�E�E�E�Ax^4-1�������Ȃ�
�Ƃ́A
�e�����������������imod2�j�����Ƃ��A����f(x)=1+x+x^4�������Ȃ��A�Ƃ������ƁB
x^15-1����������(mod2)���܂��B
x^15-1
���@(1+x)*(1+x+x^2)*(1+x+x^4)*(1+x^3+x^4)*(1+x+x^2+x^3+x^4)
��3���ڂ�f(x)�Ȃ̂ŁAf(x)�͑�����x^15-1�������܂��B
x^t-1�̂Ƃ��At��15�̑����������������imod2)����f(x)�������ɂ������ׂ܂��B�B
��x^14-1�@
���@(x+1)^2*(x^3+x+1)^2*(x^3+x^2+1)^2�A
��x^13-1�@
���@(x+1)*(x^12+x^11+x^10+x^9+x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1)�A
��x^12-1�@
���@(x+1)^4*(x^2+x+1)^4�A
��x^11-1�@
���@(x+1)*(x^10+x^9+x^8+x^7+x^6+x^5+x^4+x^3+x^2+x+1)�A
��x^10-1�@
���@(x+1)^2*(x^4+x^3+x^2+x+1)^2�A
��x^9-1�@
���@(x+1)*(x^2+x+1)*(x^6+x^3+1)�A
��x^8-1�@
���@(x+1)^8�A
��x^7-1�A�@
���@(x+1)*(x^3+x+1)*(x^3+x^2+1)�A
��x^6-1�@
���@(x+1)^2*(x^2+x+1)^2�A
��x^5-1�@
���@(x+1)*(x^4+x^3+x^2+x+1)�A
��x^4-1�@
���@(x+1)^4�A
f(x)=1+x+x^4
�������Ɏ����Ȃ����Ƃ��킩��܂����B
������
g(x)=1+x^3+x^4
�������Ɏ����Ȃ����Ƃ��킩��܂����B
���Ȃ킿�A���n�������@f(x)=1+x+x^4�A����с@g(x)=1+x^3+x^4�@�́A�����������ł����āA
�ő����P(s)=15�̂l�n�������A�Ƃ������Ƃł��B
���Ӂ�������������������������������
�������ŕ\������Ă���x�̃x�L�Ax^0�Ax^1�Ax^2�A�E�E�E�Ax^m �́A
2�i��{f[0]�Af[1]�Af[2]�A�E�E�E�Af[m]}�̏����t���Ɏg����V���{���ɉ߂��܂���B
�܂�+x^n=-x^n�i���Ȃ킿�A+1=-1�j���̐����������Ă��܂��B
���̈Ӗ��ŁA
�@�@f(x)=f[0]+f[1]x+f[2]x^2+�E�E�E+f[m]x^m�@�@�@�if[0]=f[m]=1�j�A
�̉E�ӂ́A�ϐ�x�̊��ƍl���Ă͂����܂���B
�܂��A���R�ł����A�W��f[i]��modulo2�i���邢��mod2�A���邢�͖@2�j�̉��Z�K���ɏ]���܂��B
������������������������������������
�`�`�`�`�`�`�`�`�`�`�`�`�`�`
������Œ肵��m�ɂ��āA
�@�@s[0]=a[0]�As[1]=a[1]�A�E�E�E�E�As[m-1]=a[m-1] ���Y������[�E]�ŕ\���܂��B
��^����ƁAmod2�̐��`�Q�����A
�@�@f[0]s[i-m]+f[1]s[i-m+1]+�E�E�E�E+f[m]s[i]=0 �G �imod2�j�A
�@�@�ii=m�Am+1�Am+2�A�E�E�E�E �G f[m]��0�Af[0]��0�j�A
�ɂ��A�v�f{0,1}�̖�������A
�@�@s=(s[0],s[1],�E�E�E,s[m-1],s[m],�E�E�E)�A
�������i�ċA�I�Ɂj�����܂��B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�����m=4�ɌŒ肵�ċ�̓I�ɍl���Ă݂܂��B
�@a[0]=0�Aa[1]=0�Aa[2]��0�Aa[3]=1�@�Ƃ��܂��i�����l�j�B
���������āA
�@s[0]=0�As[1]=0�As[2]��0�As[3]=1�@�i����̎n�܂�j�B
���̂Ƃ�mod2�̐��`�Q�����́A
�@f[0]*s[0]+f[1]*s[1]+f[2]*s[2]+f[3]*s[3]+f[4]*s[4]=0�A
�@�ii=4�Ai=5�Ai=6�A�E�E�E�Gf[0]=f[4]=1�j
������4���̌��n�������A
�@f(x)=f[0]+f[1]*x+f[2]*x^2+f[3]*x^3+f[4]*x^4�A
�̌W�����A
f[0]=1�Af[1]=1�Af[2]=0�Af[3]=0�Af[4]=1�Ƃ��܂��B
���@f(x)=1+x+x^4�A
�͂��߂�i=4
�@f[0]*s[0]+f[1]*s[1]+f[2]*s[2]+f[3]*s[3]+f[4]*s[4]=0�A
���@s[0]+s[1]+s[4]=0�A
���@0+0+s[4]=0�A
���@s[4]=0
����i=5
�@f[0]*s[1]+f[1]*s[2]+f[2]*s[3]+f[3]*s[4]+f[4]*s[5]=0�A
���@0+0+s[5]=0�A
���@s[5]=0
����i=6
�@f[0]*s[2]+f[1]*s[3]+f[2]*s[4]+f[3]*s[5]+f[4]*s[6]=0�A
���@s[2]+s[3]+s[6]=0�A
���@0+1+s[6]=0�A
���@s[6]=1
����i=7
�@f[0]*s[3]+f[1]*s[4]+f[2]*s[5]+f[3]*s[6]+f[4]*s[7]=0�A
���@s[3]+s[4]+s[7]=0�A
���@1+0+s[7]=0�A
���@s[7]=1
����i=8
�@f[0]*s[4]+f[1]*s[5]+f[2]*s[6]+f[3]*s[7]+f[4]*s[8]=0�A
���@s[4]+s[5]+s[8]=0�A
���@0+0+s[8]=0�A
���@s[8]=0
����i=9
�@f[0]*s[5]+f[1]*s[6]+f[2]*s[7]+f[3]*s[8]+f[4]*s[9]=0�A
���@s[5]+s[6]+s[9]=0�A
���@0+1+s[9]=0�A
���@s[9]=1
����i=10
�@f[0]*s[6]+f[1]*s[7]+f[2]*s[8]+f[3]*s[9]+f[4]*s[10]=0�A
���@s[6]+s[7]+s[10]=0�A
���@1+1+s[10]=0�A
���@s[10]=0
����i=11
�@f[0]*s[7]+f[1]*s[8]+f[2]*s[9]+f[3]*s[10]+f[4]*s[11]=0�A
���@1+0+s[11]=0�A
���@s[11]=1�A
����i=12
�@f[0]*s[8]+f[1]*s[9]+f[2]*s[10]+f[3]*s[11]+f[4]*s[12]=0�A
���@s[8]+s[9]+s[12]=0�A
���@0+1+s[12]=0�A
���@s[12]=1
����i=13
�@f[0]*s[9]+f[1]*s[10]+f[2]*s[11]+f[3]*s[12]+f[4]*s[13]=0�A
���@s[9]+s[10]+s[13]=0�A
���@1+0+s[13]=0�A
���@s[13]=1
����i=14
�@f[0]*s[10]+f[1]*s[11]+f[2]*s[12]+f[3]*s[13]+f[4]*s[14]=0�A
���@s[10]+s[11]+s[14]=0�A
���@0+1+s[14]=0�A
���@s[14]=1
����i=15
�@f[0]*s[11]+f[1]*s[12]+f[2]*s[13]+f[3]*s[14]+f[4]*s[15]=0�A
���@s[11]+s[12]+s[15]=0�A
���@1+1+s[15]=0�A
���@s[15]=0
�E
�E
�E
����s�́A
��s[0]�As[1]�As[2]�As[3]�As[4]�As[5]�As[6]�As[7]�As[8]�As[9]�As[10]�As[11]�As[12]�As[13]�As[14]�As[15]�A�E�E�E
��0�A0�A0�A1�A0�A0�A1�A1�A0�A1�A0�A1�A1�A1�A1�A0�A�E�E�E�E�E�E
��������������܂����B
���̖������l�n��ł��邱�Ƃ��m�F������@�Ƃ��āA
�@���̐����������4�Â��A���̉��2�i���\���ƂƂ炦��10�i���ɕϊ�����ƁA1������1�`15�܂ł̐��l�����ׂ�1��Âo������B
�A���ȑ��֊��Ӂi�t�@�C�j���v�Z����ƃY���ʃсi�^�E�j��0�̈ʒu�ōő�l1�������A����ȊO�ł�1�ȉ��̈��l�������B
�܂��@�ł����A�ȉ��̂悤�ɂȂ�܂��B1�`15������Ȃ��o�����Ă��܂��B
=1+x+x^4 up.jpg)
=1+x+x^4 down.jpg)
�܂��A�̎��ȑ��֊��ӂ́A�Y���ʃт�0�̂Ƃ����1�A����ȊO�ł�0.467�̈��l�������Ă��܂��B

���������āA��`�̑Q�������琶������閳������́A�m���ɂl�n��Ȃ̂ł��B
----- �����܂Ł@20181215 -----
�G�N�Z���Ŗ�����������
�G�N�Z���Ł@f(x)=1+x+x^4�@�̓������������琶������閳������̍ŏ���1�������ii=0�`14�j������Ă݂܂��傤�B
4�̐���̏����l�Ɣr���I�_���a��g�ݍ��킹���u���b�N�}���l���܂��B
��{�`�͉��}�̒ʂ�ł��B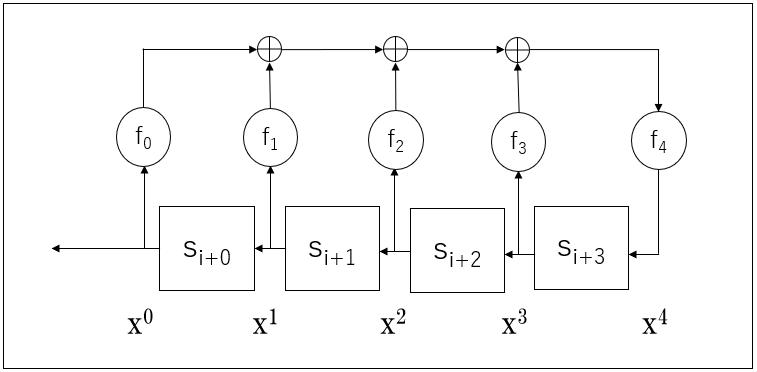
�W��f[0]=1�Af[1]=1�Af[2]=0�Af[3]=0�Af[4]=1�A�Ɓ@i=0�@�̂Ƃ��̐���̏����ls[0]=0�As[1]=0�As[2]=0�As[3]=1�A��ݒ肵�܂��B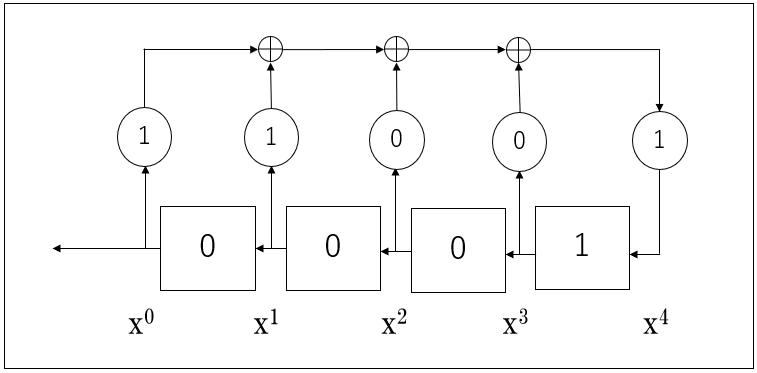
�W���́A1��0�Ȃ̂ŁA�ȉ��̂悤�ɏȗ����ď������Ƃ��ł��܂��B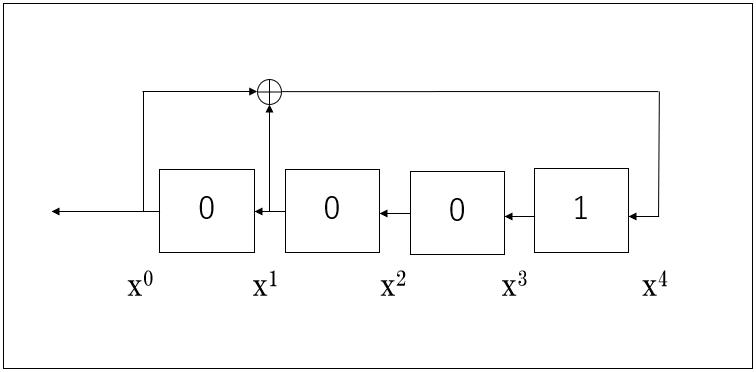
�����l0�A0�A0�A1�@���g���āAs[0]=0�As[1]=0�̔r���I�_���a����As[4]���v�Z�܂��B�G�N�Z���ł́A�_�����u=if(s(i-4)=s(i-3),0,1)�v���g���܂��B
��s[4]=if(s[0]=s[1],0,1)�A
���̂��Ƃ́A�ЂƂÂ��炵��
��s[5]=if(s[1]=s[2],0,1)�A
��s[6]=if(s[2]=s[3],0,1)�A
��s[7]=if(s[3]=s[4],0,1)�A
��s[6]=if(s[4]=s[5],0,1)�A
�E�E�E�E
�Ƃ����悤�Ɍv�Z���Ă����܂��B

���Ƃ́A���̎����ł��肩��������������Ă����܂��B
----- �����܂Ł@20181223 -----
���������������߂�
M�n�����������������́A����n��4�̏ꍇ�ɂ��ċ�̓I�Ɍv�Z���ċ��߂܂����B
������4�̂Ƃ��́Af(x)=x^(2^4-1)-1=x^15-1�̈����i�������j�̂����Ax^14-1�Ax^13-1�A�E�E�E�Ax^3-1�Ax^2-1�Ax-1���������i�������j�̂ǂ�Ƃ����ʂ��Ȃ������i�������j�������������ł����B
���A((x^15-1)/((x^14-1)*(x^13-1)*(x^12-1)*(x^11-1)*(x^10-1)*(x^9-1)*(x^8-1)*(x^7-1)*(x^6-1)*(x^5-1)*(x^4-1)*(x^3-1)*(x^2-1)*(x-1)))�Ƃ�������Z��������A���������\�t�gMaxima�ň��������i���Rmod2�ł��j���܂��B
����ƁA���ʈ����͖����̂ŁA���q�Ɏc��̂́A�����������ɂȂ�܂��B
���q�́A(x^4+x+1)*(x^4+x^3+1)�ƂȂ�A�ux^4+x+1�v�y�сux^4+x^3+1�v��2�̑����������o���ꂽ���Ƃ�������܂��B
�����̎����̕��т��t�ɂ���ƁAf[0]+��[1]x+f[2]x^2+�E�E�E�A�̌`���Ɉ�v����̂Ō��₷���Ȃ�܂��B����́A����������������̑�������Maxima�̌v�Z���ʂ̂����̂��L�q���܂����A�����������Ƃ��Ĉ����ۂɁA���̍����珬���������ŕ��ׂ��`�Ő������܂��B
��n=4�̂Ƃ��̓����������́A
�@1+x+x^4�A
�@1+x^3+x^4
�ł��B
�ł́A���X�Ɍv�Z���Ă݂܂��傤�B
n=5�̂Ƃ��A
((x^31-1)/((x^30-1)*(x^29-1)*(x^28-1)*(x^27-1)*(x^26-1)*(x^25-1)*(x^24-1)*(x^23-1)*(x^22-1)*(x^21-1)*(x^20-1)*(x^19-1)*(x^18-1)*(x^17-1)*(x^16-1)*(x^15-1)*(x^14-1)*(x^13-1)*(x^12-1)*(x^11-1)*(x^10-1)*(x^9-1)*(x^8-1)*(x^7-1)*(x^6-1)*(x^5-1)*(x^4-1)*(x^3-1)*(x^2-1)*(x-1)))
����������̕��q�́A
(x^5+x^2-1)*(x^5+x^3+1)*(x^5+x^3+x^2+x+1)*(x^5+x^4+x^2+x+1)*(x^5+x^4+x^3+x+1)*(x^5+x^4+x^3+x^2+1)
�����������́A
�@1+x^2+x^5�A
�@1+x^3+x^5�A
�@1+x+x^2+x^3+x^5�A
�@1+x+x^2+x^4+x^5�A
�@1+x+x^3+x^4+x^5�A
�@1+x^2+x^3+x^4+x^5
n=6�̂Ƃ��A
((x^63-1)/((x^62-1)*(x^61-1)*(x^60-1)*(x^59-1)*(x^58-1)*(x^57-1)*(x^56-1)*(x^55-1)*(x^54-1)*(x^53-1)*(x^52-1)*(x^51-1)*(x^50-1)*(x^49-1)*(x^48-1)*(x^47-1)*(x^46-1)*(x^45-1)*(x^44-1)*(x^43-1)*(x^42-1)*(x^41-1)*(x^40-1)*(x^39-1)*(x^38-1)*(x^37-1)*(x^36-1)*(x^35-1)*(x^34-1)*(x^33-1)*(x^32-1)*(x^31-1)*(x^30-1)*(x^29-1)*(x^28-1)*(x^27-1)*(x^26-1)*(x^25-1)*(x^24-1)*(x^23-1)*(x^22-1)*(x^21-1)*(x^20-1)*(x^19-1)*(x^18-1)*(x^17-1)*(x^16-1)*(x^15-1)*(x^14-1)*(x^13-1)*(x^12-1)*(x^11-1)*(x^10-1)*(x^9-1)*(x^8-1)*(x^7-1)*(x^6-1)*(x^5-1)*(x^4-1)*(x^3-1)*(x^2-1)*(x-1)))
����������̕��q�́A
(x^6+x+1)*(x^6+x^4+x^3+x+1)*(x^6+x^5+1)*(x^6+x^5+x^2+x+1)*(x^6+x^5+x^3+x^2+1)*(x^6+x^5+x^4+x+1)
������������
�@1+x+x^6�A
�@1+x^5+x^6�A
�@1+x+x^3+x^4+ x^6�A
�@1+x+x^2+x^5+x^6�A
�@1+x^2+x^3+x^5+x^6�A
�@1+x+x^4+x^5+x^6
n=7�̂Ƃ�
((x^127-1)/((x^126-1)*(x^125-1)*(x^124-1)*(x^123-1)*(x^122-1)*(x^121-1)*(x^120-1)*(x^119-1)*(x^118-1)*(x^117-1)*(x^116-1)*(x^115-1)*(x^114-1)*(x^113-1)*(x^112-1)*(x^111-1)*(x^110-1)*(x^109-1)*(x^108-1)*(x^107-1)*(x^106-1)*(x^105-1)*(x^104-1)*(x^103-1)*(x^102-1)*(x^101-1)*(x^100-1)*(x^99-1)*(x^98-1)*(x^97-1)*(x^96-1)*(x^95-1)*(x^94-1)*(x^93-1)*(x^92-1)*(x^91-1)*(x^90-1)*(x^89-1)*(x^88-1)*(x^87-1)*(x^86-1)*(x^85-1)*(x^84-1)*(x^83-1)*(x^82-1)*(x^81-1)*(x^80-1)*(x^79-1)*(x^78-1)*(x^77-1)*(x^76-1)*(x^75-1)*(x^74-1)*(x^73-1)*(x^72-1)*(x^71-1)*(x^70-1)*(x^69-1)*(x^68-1)*(x^67-1)*(x^66-1)*(x^65-1)*(x^64-1)*(x^63-1)*(x^62-1)*(x^61-1)*(x^60-1)*(x^59-1)*(x^58-1)*(x^57-1)*(x^56-1)*(x^55-1)*(x^54-1)*(x^53-1)*(x^52-1)*(x^51-1)*(x^50-1)*(x^49-1)*(x^48-1)*(x^47-1)*(x^46-1)*(x^45-1)*(x^44-1)*(x^43-1)*(x^42-1)*(x^41-1)*(x^40-1)*(x^39-1)*(x^38-1)*(x^37-1)*(x^36-1)*(x^35-1)*(x^34-1)*(x^33-1)*(x^32-1)*(x^31-1)*(x^30-1)*(x^29-1)*(x^28-1)*(x^27-1)*(x^26-1)*(x^25-1)*(x^24-1)*(x^23-1)*(x^22-1)*(x^21-1)*(x^20-1)*(x^19-1)*(x^18-1)*(x^17-1)*(x^16-1)*(x^15-1)*(x^14-1)*(x^13-1)*(x^12-1)*(x^11-1)*(x^10-1)*(x^9-1)*(x^8-1)*(x^7-1)*(x^6-1)*(x^5-1)*(x^4-1)*(x^3-1)*(x^2-1)*(x-1)))
����������̕��q�́A����������̕��q�́A
(x^7+x+1)*(x^7+x^3+1)*(x^7+x^3+x^2+x+1)*(x^7+x^4+1)*(x^7+x^4+x^3+x^2+1)*(x^7+x^5+x^2+x+1)*(x^7+x^5+x^3+x+1)*(x^7+x^5+x^4+x^3-1)*(x^7+x^5+x^4+x^3+x^2+x+1)*(x^7+x^6+1)*(x^7+x^6+x^3+x+1)*(x^7+x^6+x^4+x+1)*(x^7+x^6+x^4+x^2+1)*(x^7+x^6+x^5+x^2+1)*(x^7+x^6+x^5+x^3+x^2+x+1)*(x^7+x^6+x^5+x^4+1)*(x^7+x^6+x^5+x^4+x^2+x+1)*(x^7+x^6+x^5+x^4+x^3+x^2+1)
������������
�@1+x+x^7�A
�@1+x^3+x^7�A
�@1+x^4+x^7�A
�@1+x^6+x^7�A
�@1+��+x^3+x^6+x^7�A
�@1+��+x^4+x^6+x^7�A
�@1+x+x^2+x^3+x^7�A
�@1+x^2+x^3+x^4+x^7�A
�@1+x+x^2+x^5+x^7�A
�@1+x+x^3+x^5+x^7�A
�@1+x^3+x^4+x^5+x^7�A
�@1+^2+x^4+x^6+x^7�A
�@1+x^2+x^5+x^6+x^7�A
�@1+x^4+x^5+x^6+x^7�A
�@1+x+x^2+x^3+x^4+x^5+x^7�A
�@1+x+x^2+x^3+x^5+x^6+x^7�A
�@1+x+x^2+x^4+x^5+x^6+x^7�A
�@1+x^2+x^3+x^4+x^5+x^6+x^7
n=8�̂Ƃ�
((x^255-1)/((x^254-1)*(x^253-1)*(x^252-1)*(x^251-1)*(x^250-1)*(x^249-1)*(x^248-1)*(x^247-1)*(x^246-1)*(x^245-1)*(x^244-1)*(x^243-1)*(x^242-1)*(x^241-1)*(x^240-1)*(x^239-1)*(x^238-1)*(x^237-1)*(x^236-1)*(x^235-1)*(x^234-1)*(x^233-1)*(x^232-1)*(x^231-1)*(x^230-1)*(x^229-1)*(x^228-1)*(x^227-1)*(x^226-1)*(x^225-1)*(x^224-1)*(x^223-1)*(x^222-1)*(x^221-1)*(x^220-1)*(x^219-1)*(x^218-1)*(x^217-1)*(x^216-1)*(x^215-1)*(x^214-1)*(x^213-1)*(x^212-1)*(x^211-1)*(x^210-1)*(x^209-1)*(x^208-1)*(x^207-1)*(x^206-1)*(x^205-1)*(x^204-1)*(x^203-1)*(x^202-1)*(x^201-1)*(x^200-1)*(x^199-1)*(x^198-1)*(x^197-1)*(x^196-1)*(x^195-1)*(x^194-1)*(x^193-1)*(x^192-1)*(x^191-1)*(x^190-1)*(x^189-1)*(x^188-1)*(x^187-1)*(x^186-1)*(x^185-1)*(x^184-1)*(x^183-1)*(x^182-1)*(x^181-1)*(x^180-1)*(x^179-1)*(x^178-1)*(x^177-1)*(x^176-1)*(x^175-1)*(x^174-1)*(x^173-1)*(x^172-1)*(x^171-1)*(x^170-1)*(x^169-1)*(x^168-1)*(x^167-1)*(x^166-1)*(x^165-1)*(x^164-1)*(x^163-1)*(x^162-1)*(x^161-1)*(x^160-1)*(x^159-1)*(x^158-1)*(x^157-1)*(x^156-1)*(x^155-1)*(x^154-1)*(x^153-1)*(x^152-1)*(x^151-1)*(x^150-1)*(x^149-1)*(x^148-1)*(x^147-1)*(x^146-1)*(x^145-1)*(x^144-1)*(x^143-1)*(x^142-1)*(x^141-1)*(x^140-1)*(x^139-1)*(x^138-1)*(x^137-1)*(x^136-1)*(x^135-1)*(x^134-1)*(x^133-1)*(x^132-1)*(x^131-1)*(x^130-1)*(x^129-1)*(x^128-1)*(x^127-1)*(x^126-1)*(x^125-1)*(x^124-1)*(x^123-1)*(x^122-1)*(x^121-1)*(x^120-1)*(x^119-1)*(x^118-1)*(x^117-1)*(x^116-1)*(x^115-1)*(x^114-1)*(x^113-1)*(x^112-1)*(x^111-1)*(x^110-1)*(x^109-1)*(x^108-1)*(x^107-1)*(x^106-1)*(x^105-1)*(x^104-1)*(x^103-1)*(x^102-1)*(x^101-1)*(x^100-1)*(x^99-1)*(x^98-1)*(x^97-1)*(x^96-1)*(x^95-1)*(x^94-1)*(x^93-1)*(x^92-1)*(x^91-1)*(x^90-1)*(x^89-1)*(x^88-1)*(x^87-1)*(x^86-1)*(x^85-1)*(x^84-1)*(x^83-1)*(x^82-1)*(x^81-1)*(x^80-1)*(x^79-1)*(x^78-1)*(x^77-1)*(x^76-1)*(x^75-1)*(x^74-1)*(x^73-1)*(x^72-1)*(x^71-1)*(x^70-1)*(x^69-1)*(x^68-1)*(x^67-1)*(x^66-1)*(x^65-1)*(x^64-1)*(x^63-1)*(x^62-1)*(x^61-1)*(x^60-1)*(x^59-1)*(x^58-1)*(x^57-1)*(x^56-1)*(x^55-1)*(x^54-1)*(x^53-1)*(x^52-1)*(x^51-1)*(x^50-1)*(x^49-1)*(x^48-1)*(x^47-1)*(x^46-1)*(x^45-1)*(x^44-1)*(x^43-1)*(x^42-1)*(x^41-1)*(x^40-1)*(x^39-1)*(x^38-1)*(x^37-1)*(x^36-1)*(x^35-1)*(x^34-1)*(x^33-1)*(x^32-1)*(x^31-1)*(x^30-1)*(x^29-1)*(x^28-1)*(x^27-1)*(x^26-1)*(x^25-1)*(x^24-1)*(x^23-1)*(x^22-1)*(x^21-1)*(x^20-1)*(x^19-1)*(x^18-1)*(x^17-1)*(x^16-1)*(x^15-1)*(x^14-1)*(x^13-1)*(x^12-1)*(x^11-1)*(x^10-1)*(x^9-1)*(x^8-1)*(x^7-1)*(x^6-1)*(x^5-1)*(x^4-1)*(x^3-1)*(x^2-1)*(x-1)))
����������̕��q�́A
(x^8+x^4+x^3+x^2+1)*(x^8+x^5+x^3+x+1)*(x^8+x^5+x^3+x^2+1)*(x^8+x^6+x^3+x^2-1)*(x^8+x^6+x^4+x^3+x^2+x+1)*(x^8+x^6+x^5+x-1)*(x^8+x^6+x^5+x^2-1)*(x^8+x^6+x^5+x^3-1)*(x^8+x^6+x^5+x^4+1)*(x^8+x^7+x^2+x+1)*(x^8+x^7+x^3+x^2+1)*(x^8+x^7+x^5+x^3+1)*(x^8+x^7+x^6+x+1)*(x^8+x^7+x^6+x^3+x^2+x+1)*(x^8+x^7+x^6+x^5+x^2+x+1)*(x^8+x^7+x^6+x^5+x^4+x^2+1)
������������
�@1+x^2+x^3+x^4+x^8�A
�@1+x+x^3+x^5+x^8�A
�@1+x^2+x^3+x^5+x^8�A
�@1+x^2+x^3+x^6+x^8�A
�@1+x+x^5+x^6+x^8�A
�@1+x^2+x^5+x^6+x^8�A
�@1+x^3+x^5+x^6+x^8�A
�@1+x^4+x^5+x^6+x^8�A
�@1+x+x^2+x^7+x^8�A
�@1+x^2+x^3+x^7+x^8�A
�@1+x^3+x^5+x^7+x^8�A
�@1+x+x^6+x^7+x^8�A
�@1+x+x^2+x^3+x^4+x^6+x^8�A
�@1+x+x^2+x^3+x^6+x^7+x^8�A
�@1+x+x^2+x^5+x^6+x^7+x^8�A
�@1+x^2+x^4+x^5+x^6+x^7+x^8�A
�Ƃ肠�����A�茳�ɂ��铹��iMaxima�j�ł����܂ł���Ă݂܂����B
n�������������̕\�����@
n���̓������������u���b�N�}�ɓW�J����Ɖ��}�̂悤�ɂȂ�܂��B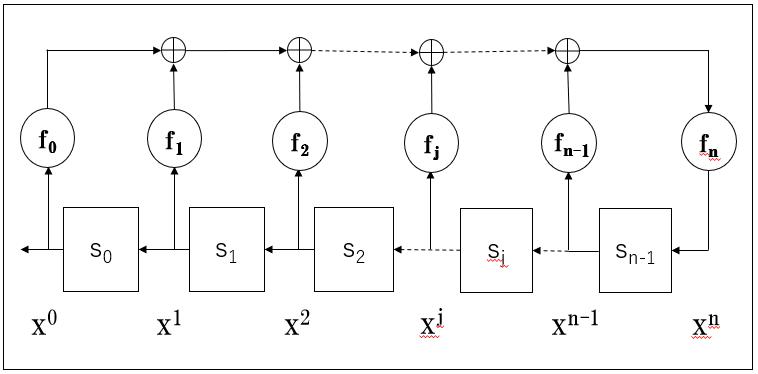
�����������̕\�����@�͂��낢�날��悤�ł����A
f(x)=f[0]1+��[1]x+.f[2]x^2�E�E�E+f[j]x^j+�E�E�E+f[n-1]x^(n-1)+f[n]x^n
�̕\���̂ق��ɁAf[0]��f[n]�������W����1�ɂȂ�f[j]��j�����������ʂɕ��ׂ���@������܂��B
�Ⴆ�An=5�̂Ƃ���
�@1+x^3+x^5�@�́@(3)�A
�@1+x+x^2+x^3+x^5�@�́@(1,2,3)�A
�ƕ\�����܂��B
n=4�`8�̈ꗗ�\������Ă݂܂��B
n��4�`24�̈ꗗ�\���l�b�g�Ō������̂ŏЉ�܂��B���̕\�ɂ�n=4�������ĈӐ}�I��j��3�̑g�ݍ��킹�����L�q����Ă��܂���B����́AM�n��𗐐��ƂƂ炦��ƁAj��3�̂Ƃ��̐��������̑g�ݍ��킹�̂Ƃ��̐��������ƂĂ��ǂ����炾�����ł��B
����ɁAn��4�`8�̕�����2�̕\���r����ƁAMaxima�ŋ��߂������������̂��ׂĂ����グ���Ă��Ȃ����Ƃ�������܂��B����������Ƃ��Ă̐��������̑I�����ꂽ���ʂȂ̂ł��傤���H

���Ȃ݂ɁAn=24��M�n��̎����́@16,777,216-1�@�ł��B
������Ă����������Ɏv���܂����Aintel��CPUcorei7�̃N���b�N���g����3GHz�`4GHz�ł��̂ŁA��0.005�b���ł��B
----- �����܂Ł@20181229 -----
�f�B�W�^����H��M�n��M������낤
�l�n��́A�V�t�g���W�X�^�Ɣr���I�_���a�iEX-OR�j�̑g�ݍ��킹�Ńn�[�h�E�F�A�Ƃ��Ă����ł���Əq�ׂ܂����B�ǂ̂悤�ɍ\��������f�B�W�^����H��M�n��M�����ł��邩�������Ă݂܂��B
IC�i�W�ω�H�j��74�V���[�Y������܂��B1962�N�Ƀe�L�T�X�E�C���X�c�������c�Ђ��������͂��߂��P�d��[+5V]�œ��삷��ėpIC�ŁA74�Ŏn�܂�4���܂���5���̌^�Ԃ��t���Ă��邽��74�V���[�Y�ƌĂ�Ă��܂��B
7486���r���I�_���a�iEX-OR�j�œ��͒[�q2�E�o�͒[�q1�̂��̂�4�z�u����Ă��܂��B
�܂��A74164��8�r�b�g�̃V�t�g���W�X�^�ł��B
���̃V�t�g���W�X�^�͏����l��ݒ�ł��܂���̂ŁA�d���X�C�b�`����ꂽ�Ƃ��Ɋe�r�b�g�ɋ��R�ɐݒ肳�ꂽ�l�i1��0�j�������l�Ƃ���M�n������邱�ƂɂȂ�܂��B�����A���̓d����������8�r�b�g�S����0�ɐݒ肳��Ă��܂�����AM�n��͔������܂���B���̂Ƃ��́A�d��������������āA�ē������Ă݂邱�ƂɂȂ�܂��B
���R�̏����l�ݒ肪���ȂƂ��́A74195��4�r�b�g�V�t�g���W�X�^���g���܂��B���[�h�M������͂����4�r�b�g�̏����l�ݒ�i�C�ӂ�1��0�j���ł��܂��B
�V�t�g���W�X�^�̃f�[�^�̈ړ��i�V�t�g�j�́A���͂���N���b�N�̗����オ��̃^�C�~���O�ōs���܂��B
�N���b�N�Ƃ́H
���ėpIC�̒��ŁA�V�t�g���W�X�^��J�E���^���́A�O��������͂����N���b�N�Ƃ�����`�g�̐M���̗����オ��i�܂��͗�����j�̃^�C�~���O�ň�ē��삷��悤�ɐv����Ă��܂��B���̋�`�g�̉��i0V�j�Ɠʁi5V�j��1�g��1�������`�����āA1�b�Ԃ�1��̉��ʂ�1Hz�i1�w���c�j�Ɛ����܂��B
7486�A74164�y��74195�̃s���z�u�͉��}�̒ʂ�ł��B
.jpg)
.jpg)
.jpg)
�d���͒���+5V�łucc�ɋ������܂��B
���āA8�r�b�g�V�t�g���W�X�^��EX-OR�ŁA����n=8��M�n��M��������H��v���Ă݂܂��B
8���̓����������̂Ȃ�����Af(x)=1+x^3+x^5+x^7+x^8���g���Ă݂܂��傤�i3,5,7)�B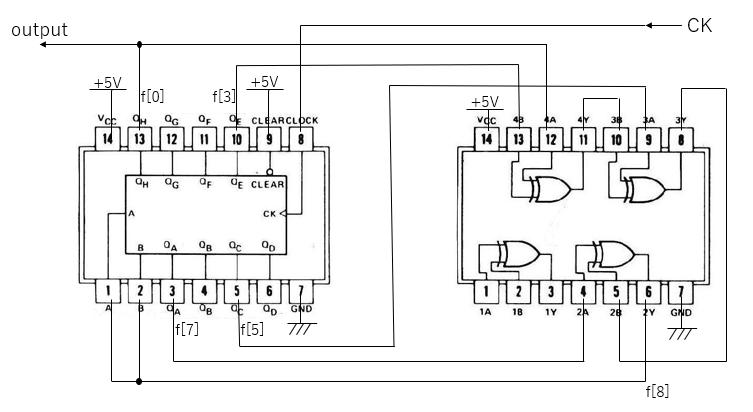
�N���b�N�iCK�j���g���́A74HC164�̃^�C�v�ōő�21MHz�ł��B
HC�Ƃ́H
���m�[�}���^�C�v�i���̏ꍇ74164�j�������d�͂���H�̔������x�����������̃^�C�v
�N���b�N������H�́AIC�̃C���o�[�^�i�_���ے�j�Ɛ������U�q�A��R�ƃR���f���T�ō쐬���܂��B
74HCU04���g�����z���}�͈ȉ��̒ʂ�ł��B
20MHz�ȉ��̃N���b�N���쐬����ۂ̒�R�A�R���f���T�̒l�͈ȉ��̒ʂ�ł��B
�d�q���i�͓���ł���H
 74HCU04�@1��30�~
74HCU04�@1��30�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 74HC86�@1��30�~
74HC86�@1��30�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 74HC164�@1��30�~
74HC164�@1��30�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 �����U���q20MHz�@1��30�~
�����U���q20MHz�@1��30�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 +5V�����X�C�b�`���O�d���@1��3,690�~
+5V�����X�C�b�`���O�d���@1��3,690�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 �J�[�{����R�i�Y�f�햌��R�j1M���@1�܁i100�{����j100�~
�J�[�{����R�i�Y�f�햌��R�j1M���@1�܁i100�{����j100�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 �Z���~�b�N�R���f���T22pF�@1��5�~
�Z���~�b�N�R���f���T22pF�@1��5�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 �u���b�h�{�[�h�@270�~
�u���b�h�{�[�h�@270�~
�yPR�����p�z�������������Ƃ������Ɏ��s�ł���u���b�h�{�[�h�B �d�q��H�̕���A��H�̑g�݊����������ɂł��܂��B �ȒP�ȉ�H�̎����A���i�̍����ւ��������ɂ�������H�A�b�q�̒萔���߂⍂���ȃp�[�c�̕]���ɂ��œK�ł��B �͂��Ă��g�p���Ȃ��̂ł₯�ǂ̐S�z������܂���B
 �y�g�p��z
�y�g�p��z
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
 �u���b�h�{�[�h�p�W�����p���C���Z�b�g�i10cm�j�@18�{180�~
�u���b�h�{�[�h�p�W�����p���C���Z�b�g�i10cm�j�@18�{180�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�f�B�W�^���I�V���X�R�[�v�͓d�q���i�ł͂���܂��A��H�̍쐬�r����IC������ɍ쓮���Ċ�]����M���g�`����������Ă��邩�m���߂邱�ƂɎg���܂��B�܂��AM�n��M����������Ɣ������Ă��邩�̊m�F�ɂ��g���܂��B
��������20MHz�̐M���𑪒肷��̂�200MHz�̑ш�����I�V���X�R�[�v���K�v�H�Ǝv���ł��傤���A�M���̒x�����Ńq�Q�ƌĂ�鈫��������i�m�b�I�[�_�[�̃p���X���������邱�Ƃ�����̂ŁA����������邽�߂ɕK�v�ɂȂ��Ă��܂��B
 �f�B�W�^���I�V���X�R�[�v200MHz�@54,000�~
�f�B�W�^���I�V���X�R�[�v200MHz�@54,000�~
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
30�~+30�~+30�~+30�~+3,690�~+100�~+5�~+5�~+270�~+180�~+54,000�~=58,370�~
�y�H���d�q�ʏ��z�̒ʐM�̔��ōw���\�ł��B
���@�@�@���@�@�@��
http://akizukidenshi.com/catalog/
----- �����܂Ł@20190107 -----
��H�V�~�����[�^���g��
�߂����ɂ��Ȃ��d�q�H��̂��߂����ɁA3��~�ȏ������d��������A5���~�ȏ������I�V���X�R�[�v���̂͂Ȃ�Ƃ����������Ȃ��̂ŁA��H�V�~�����[�^���g�����Ƃɂ��܂��B
���݁A�茳�ɂ���̂́A�uCD-ROM�t �d�q��H�V�~�����[�^���� ����Łv (�u���[�o�b�N�X)�y2005�N9��21�������F�艿1,600�~�z�ł��BCD-ROM�Ɏ��^����Ă���̂�CircuitMaker Student�łŁA��x�ɑg�߂�f�q����50�܂łƂ��������͂���܂��B����ł��A�Ȃ��Ȃ��̗D����̂��Ǝv���܂��B
�u�L���ł�CircuitMaker�͓d�q��H����̋��ނƂ��Ďg���₷���l�C������܂������C �̔�����Altium�Ђ͂��̐��i��̔����~�ɂ��AStudent�ł̖����z�z����~���Ă��܂��܂����B2007�N10���̎��_�ŁA���łɁACircuitMaker����̗B��̕��@���u�k�Ѓu���[�o�b�N�X���w�����邱�Ɓv�E�E�Ƃ����L��������܂����B
�ł��̂ŁACircuitMaker �ɋ����������A�������]����Ƃ��ɂ́Aamazon�����璆�Ö{�uCD-ROM�t �d�q��H�V�~�����[�^���� ����Łv (�u���[�o�b�N�X)���w�����邵���Ȃ��悤�ł��B
amazon�Ō������܂����B�u���Õi-�v��124�~�A����257�~�ō��킹��381�~�Ŕ����Ă��܂����B
�����ɔ����Ă݂܂����B�u���Õi-�v�Ƃ����̂ŁA���Ă��A�������ݓ�����̂��Ǝv���Ă��܂������A�V�i�̂悤�ł����̂Łu���������A���������v�Ɗ��ł��܂�����ACD-ROM������܂���B�u����͂Ȃ������v�E�E��������ł��B
���Õi�ɂ͓�����A�O�ꂪ����Ƃ������Ƃł��ˁB�i����Ƃ��ACD-ROM�́ACD�Ƃ���amazon�ŕʔ���H�H�j
���łɔ̔��I���������̂��g���̂͂������Ȃ��̂��H�Ǝv������́A�C���^�[�l�b�g��ɂ�CircuitMaker�ȊO�̑��푽�l�Ȗ����̓d�q��H�V�~�����[�^������悤�Ȃ̂ŁA������ŃV�~�����[�g����̂��ǂ��ł��傤�B

PC��CircuitMaker Student�ł��C���X�g�[�����܂����B���삪�ۏ���Ă���WindowsXP����3���������Ă���Windows10�ł����A����ƂȂ������Ă��܂��B10�Ɉڍs����ۂɓ����Ȃ��Ȃ�\�t�g������ق炠�����Ƃ̉\���������̂ŐS�z���Ă��܂����B���v�̂悤�ł��B
CircuitMaker�ō\�z������H�̓V�~�����[�V�����X�^�[�g���̏����l���I�[���h�[���h�Ȃ̂ŁAM�n��������܂���B�����ŏ����l���ݒ�ł���74LS195��4�r�b�g�V�t�g���W�X�^���g���ȉ��̂悤�ɉ�H��g�݂܂����B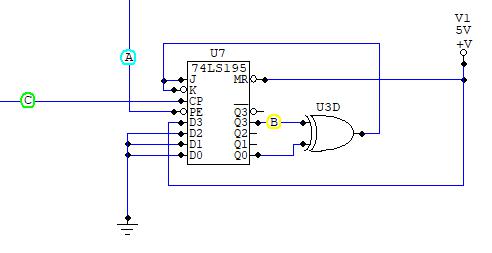
���u�b�i�ΐF�j�v�F�N���b�N�M���B
���u�`�i���F�j�v�F���[�h�M���B
�@���M���h�k�h�i=0V�j�̂Ƃ���4�r�b�g�V�t�g���W�X�^�ɏ����lD3=1�AD2=0�AD1=0�AD0=0�A���ݒ�B
���u�a�i���F�j�v�FM�n��̏o�͐M���B
74LS195��1�����g�킸�An=4�̓���������f(x)=1+x^3+x^4�i������ɕ\����(3)�j�A����=15��M�n��ɂ����̂́A�f�B�W�^���I�V���X�R�[�v�ɐM���̑S�̑���\�����āAM�n��M�����m���ɔ������Ă��邱�Ƃ��m�F���₷�����邽�߂ł��B
���̂Ƃ��̃f�B�W�^���I�V���X�R�[�v��ʂ͈ȉ��̒ʂ�ł��B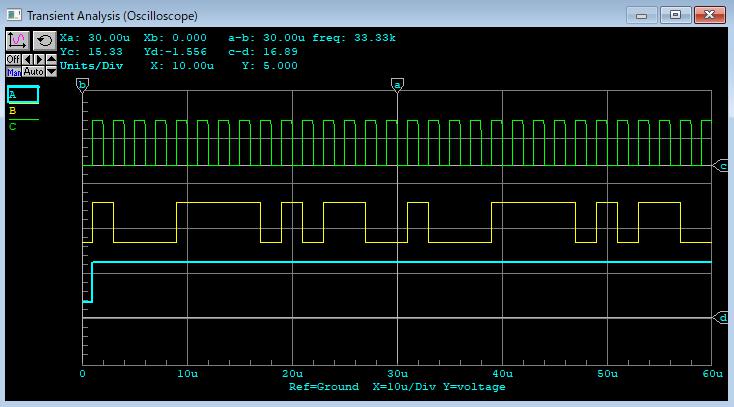
����������f(x)=1+x^3+x^4�A�����l1�A0�A0�A0��1�����i=15�j����M�n��́A
1�A0�A0�A0�A1�A1�A1�A1�A0�A1�A0�A1�A1�A0�A0�B
�I�V���X�R�[�v�̐M���Ɣ�r���āE�E�E�A
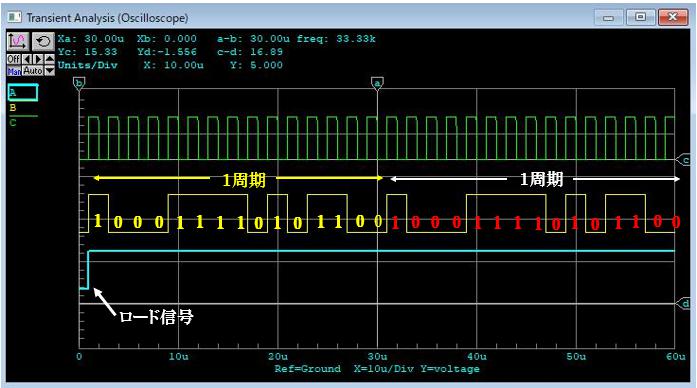
���v���Ă��܂��B�i�悩�����A�悩�����j
���Ȃ݂ɁA���̐M���͂l�n��ƌ��߂��Ă��܂����A�m���߂Ă݂܂��B
=1+x^3+x^4 up.jpg)
=1+x^3+x^4 down.jpg)
1�`15�܂ł̐������o�����Ă��܂��B

���ȑ��֊��ӂ���=0�ōő�l1�������A���̑���1��菬�������l�������Ă��܂��B
�l�n��M�������Ă��邱�Ƃ��m�F�ł��܂����B�i�ĂсA�悩�����A�悩�����j
----- �����܂Ł@20190119 -----
M�n��̌n��
M�n�獂�x�ɐi�������[�����������A���S���Y���Ƀ����Z���k�E�c�C�X�^�i�ȉ�MT�j������܂��B
����MT��2�l�̓��{�l�A���{�����Ɛ�����m���ɂ���ĊJ������܂����B
�������A�^�����������A���S���Y���Ƃ��Č��ݍł������]���Ă��܂��B
���{���Ɛ������́AMT���l�Ă���O�ɁAM�n��W������Twisted General Feedback Shift Register(�ȉ�TGFSR)���Ă��܂����B
�����
x[n+p]=x[n+q]+x[n]�`�@�@ (p>q>0)�@�@(1)�A
��p���ċ^������������܂��B
�������` ��Twister�ƌĂ�� GF(2)�i���K���A�́AM�n��������̂����炱���Ȃ�܂���ˁj �̌��i��1��0�j��v�f�Ƃ��� �ց~�� �̍s��i���l�I�ɂ͍s��\���͋��j�ł��B
������ x[n]��GF(2)^�� �i���ǂ��䂤���ƁH�j�ł��B
TGFSR�� 2^(p��)-1 �̍ő�����������܂��B�܂��v�Z�������ɂȂ�悤�� �`��I�����邱�Ƃ��ł��܂��B
TGFSR�����ǂ������̂�MT�ŁA�ȉ��ɂ��^������������܂��B
x[n+p]=x[n+q]+x[n+1]�a+x[n]�b (p>q>0)�@�@(2)�A
��(2)�ɂ��ő������ 2^(19937)-1 �̂Ƃ��A����MT19937�ƌĂꂢ�܂��B���ʂ�MT�Ƃ����Ƃ��́AMT19937���w���܂��B
----- �����܂Ł@20190122 -----