アナログコンピュータ update 20200808
なぜアナログコンピュータ?
「ステイホーム」をきっかけにアナログコンピュータに興味を持ったのですが、検索に頓挫したので、見つからないなら自分で考えてみようと思った次第です。
運動方程式を解けるのか
電子回路でアナログコンピュータを作るときに肝となるのが演算増幅器(Operational amplifier:通称オペアンプ)です。
ディジタルコンピュータに何かをやらせようとしたとき、目的に応じたプログラムを書きますが、アナログコンピュータではオペアンプや抵抗、コンデンサなどを目的に応じて組み合わせて実現します。
したがって、運動方程式を使って何を求めるかによって、アナログコンピュータでは回路の組み方が違ってきます。
例えば、重力が存在する地上において、
1.一定の速度を持つ物体をある射角で打ち出した場合、どこまで上がるのか、どこまで飛ぶのか、
という問題と、
2.目標までの距離がわかっている場合に、一定の速度で打ち出す物体をその目標に到達させたいときの射角はいくらか、
という問題では回路の組み方は違ってきます。
また、オペアンプと抵抗、コンデンサの組み合わせでできる演算は、加法、減法、積分、微分、定数倍の乗算(増幅)であり、いわゆる乗算、除算はできないという特徴があります。
アナログの専用の乗算IC、除算ICはありますが、ここではとりあえずオペアンプで何とかしてみようと思っております。
【空気抵抗のない場合】
■重力加速度g、射角θ、初速S0の場合の最高高度と飛翔距離を求めてみます。
【速度の表記は普通はVで表現しますが、電気回路を扱うときは電圧もVで表記するので、混乱しないように速度の方を今回だけはSとします】
重力加速度の方向を-y軸、y軸と直角な方向をx軸とするxy平面内での運動を考える。x軸とy軸の交わる点を原点として、そこから射角θ、初速S0で打ち出します。
x軸方向のt秒後の位置は、x=S0*(cosθ)*∫dt 【積分範囲;0→t】・・・①
y軸方向のt秒後の位置は、y=S0*(sinθ)*∫dt-g*∫∫dtdt 【積分範囲;0→t】・・・②
y軸方向のt秒後の速度は、Vy=S0*(sinθ)-g*∫dt 【積分範囲;0→t】・・・③
式①と式②はそのままの形でオペアンプを使った回路に置き換えられます。式③も①②の回路からそもまま作れます。
オペアンプの記号は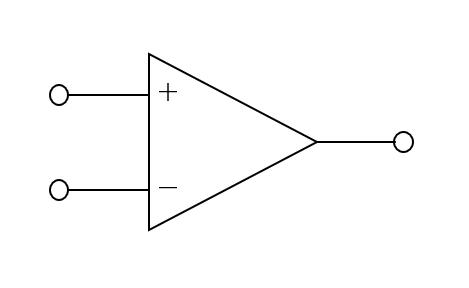
オペアンプの動作は
Vin=V1-V2, Vout=A*Vin ,A;増幅率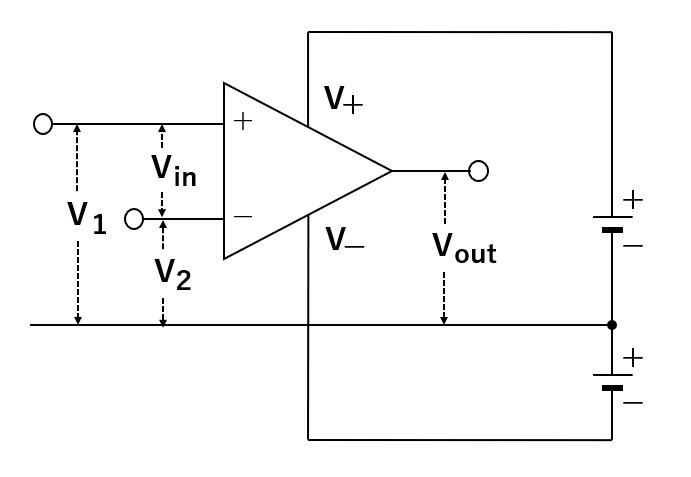
ICパッケージ化されたDIPタイプのオペアンプの外観は次の通りです。
このDIPパッケージのピン配置は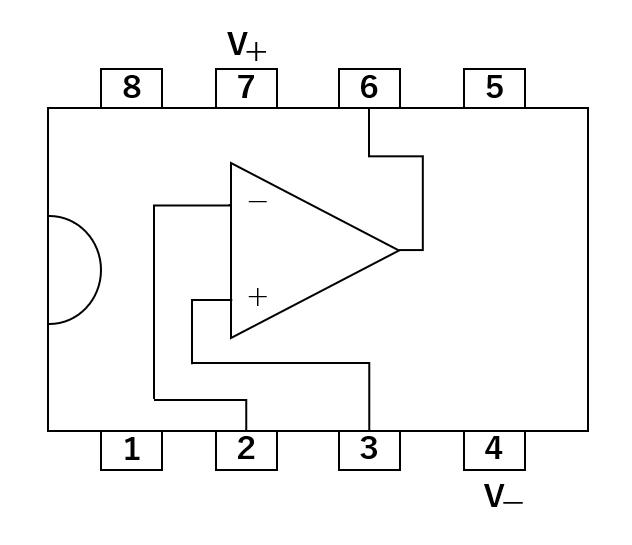
このオペアンプを使った積分回路は
【積分回路の図】
式①は
【式①を電子回路に置き換えた図】
式②は
【式②を電子回路に置き換えた図】
式③は
【式③を電子回路に置き換えだ図】
この回路達を使って、題意の「最高高度と飛翔距離」を求めなければなりません。
それには回路的なテクニックを使います。
最高高度に達した時は②は最大電圧を記録して、後はどんどん電圧を降下させていきます。この最大値を検知してその値を保持(ホールド)する回路を考えます。
【最大値検知+ホールド回路の図】
または、③の速度が0になった時を検出して、その時の②の電圧を保持する回路を考えます。
【速度0を検知してその時の②をホールドする回路の図】
次に②は打ち出された時の高度は0で、再び0になった時にx軸に着地したことになります。
②の高度が0になった時を検出して、その時の①の電圧を保持する回路を考えます。
これは先ほどの回路がそのまま応用できます。
【高度0を検知してその時の①をホールドする回路の図】
あと、計算をスタートさせるスイッチと、計算前にはコンデンサCに溜まっている電荷を放電しておくスイッチも必要です。
【スタートスイッチと放電スイッチの図】
全部繋げてみましょう。
【全部繋げた図】