����V��
�i���{���j^���̂Ƃ��́A���Ƃ��̌W���������O�̏ꍇ�A�����P�̏ꍇ�A�����Q�E�E�E�Əォ��s���~�b�h�̂悤�ɕ��ׂĂ����ƁA�p�X�J���̎O�p�`������Ă��܂��B�W�J�̌W�����O�p�`��ɕ��ׂ����̂Ƃ����̂������ł����A�f���C�Ȃ����������ł��ˁB
�O�p�`���`��鐔���́A�i���{���j�~�i���{���j�~�E�E�E�ƌv�Z�����Ă����Ȃ��Ƃ��A�W�����m�̊ȒP�ȑ����Z�łł���̂��~�\�ł��B�܂��A�W�����ȒP�Ɏ��o����A��������Ȃ��A�O�p�`���`��鐔���̕��ѕ��̐������̂��̂��������낢�悤�ł��B
���������郋�[���Ɋ�Â��ĕ��ׂĂ����ƁA�����[�����������o�����Ƃ�����悤�ł����A���ꂪ�厩�R���̂Ȃ��ɂ���Ȃ�炩�̒����Ǝ��ʂ��Ă����肷��ƁA���炽�߂Ă͂��Ƃ���̂ł��B�u�������낢�v�Ǝv�����炵�߂����̂ł��傤�B
�p�X�J���̎O�p�`���A�p�X�J���ȑO�ɂ���������Ă��āA�p�X�J���͂��̐��ʂ��܂Ƃ߂ďo�ł����̂ŁA���̂悤�Ȗ��O�����Ă���悤�ł��B
���̎O�p�`�ɂ́A�����u�Ɍ��O�p�`�v�܂��́u�k�P�O�p�`�v�A�C�����u�n�C���[���̎O�p�`�v�A�C�^���A�u�^���^���A�̎O�p�`�v�Ǝ����ꏊ�ɂ���Ă��܂��܂Ȗ��O���t�����Ă���݂����ł��B
�����ȍ~�A���m�Ƃ�������ʂ��ċߑ㕶����������Ă������{�́u�p�X�J���v�Ƃ������m�l�̖��O�̕t�����O�p�`�Ƃ��ė������Ă����킯�ł��B
----- �����܂� 20140709 -----
����W��
�N���X�̗F�B�������̐Ȃ̍�����ł킢�킢����Ă��閲�����Ă��郍�o�[�g�ł��B
��l�ɂЂƂÂ��ƈ֎q�������āA���ɒN������̂��ł悭���߂��A�w���̂͂��߂̐ȑւ��̂��Ƃ��v�������ׂ܂����B
�Ƃ��낪�A�y�[�W�̓r���̑}�G���݂�ƒ������ɕ���ō����Ă���G���̂��Ă��܂��B����������邽�߂̏Â���ŕ֗��ȗl�q������͎̂��R�����A�܂��Ė��̒��Ƃ����b�ł����B
�F�B���o�Z���ċ����ɂ���Ă��邽�тɁA���̎��̐l���łł��邷�ׂĂ̕��ו��������o���Ƃ��A���̑g�����̐��̑������͊K��ŕ\�����Ƃ��ł���Ƃ������Ƃł��B�����ɂR�l����Ă���R�̊K�恁�R�~�Q�~�P���R�I�A�T�l����T�̊K�恁�T�I�B
�����ł��A��l�ЂƂ肪������ł������̂�����ŁA�w�����Ƃ̐ȑւ��ł́A�R�l�ł�����������Ȃ����Ă��Ƃł��B
�܂��āA�P�O�l�̃N���X�ƂȂ�ƂR�C�U�Q�W�C�W�O�O�ʂ�̍����������킯�ŁA�P���P��̐ȑւ��ł��i�y���Ȃ��Ŋw�Z�ɍs���Ƃ��Ă��j�X�C�X�S�Q�N������܂��B
�����A���ׂĂ̍�����̍Ō�̎p���������Ǝv������A�ꕶ���ォ��ȑւ����͂��߂Ȃ��Ƃ����Ȃ��킯�ł��B
�P�����Ƃɐȑւ������ĂU�O�C�S�W�O���ԁA���W������P�Q���܂ŁA���H��H�ׂ���P������R���܂łU���Ԃ�葱����ƂP�O�C�O�W�O���A�y�����x�܂��ȑւ��𑱂��āA�Q�W�N������܂��B
���w�Z�ɓ��w�������̓�����P�����Ƃɐȑւ��𑱂��Ă��A���ꂾ�����Ђ������葱���Ă��A���w�Z�̑��Ƃ܂łɂ͋ɂ߂��Ȃ����̍��肩��������킯�ŁA�w���̕ς��ڂɂ��������Őȏ������߂Ȃ���Κ��������Ȃ��킯�Ȃ̂ł��ˁB
�Z���|������l���̂��Ƃőg�����̘b������̂ł����A�����Ƀp�X�J���̎O�p�`���o�Ă��܂��B���łɑg�����̐��̓p�X�J���̎O�p�`�̒��ɂ�����Ă���E�E�E�����w�I�ȓ���������O�p�`�Ȃ�ł��ˁB
�p�X�J���Ƃ����A���E�ōŏ��ɋ@�B���̌v�Z�@������������ł��B�Ŗ������ł����������c��Ȍv�Z�ɋꂵ�ނ̂��݂āA�p�X�J���P�U�˂̂Ƃ��ɍl�Ă��R�N�������č쐬���������ł��B
���̌v�Z�@�̎q���̂ЂƂ��d��ŁA����̊K��̌v�Z�ɂ��P�Q���̓d������g���Ă��܂��B�p�X�J���̌v�Z�@�́A�����Z�����ł������A�d��͈����Z�A�|���Z�A����Z�A���������v�Z���܂��B�������ɂS�O�O�N�̍�������̂ł����A�p�X�J���̎O�p�`�ƂƂ��ɂ��̉��b�͏\���ɎĂ���܂��B
----- �����܂� 20140712 -----
����X��
�����̘b�ł��B
�Ñ�M���V���l�͖����̘b���I���ɔ����Ă��܂����B�p���h�b�N�X�Ɋׂ邩��ł��B
�[�m���̃p���h�b�N�X�͗L���ł��B�Ñ�M���V���_�b�̒��ōő��̃A�L���X�Ƃ����ǂ��A�L���X�̑O��i�ދT��ǂ��������Ƃ͂ł��Ȃ��Ƃ������̂ł��B
����l�Ƃ����ǂ��A������Ƃ₻���Ƃł͂��̃p���h�b�N�X��_�j����͓̂���B���̎������瓦��邱�Ƃ��o����悤�ɂȂ����̂͂����ŋ߂̂��Ƃ��Ƃ������Ƃł��B
�����̔����͖����E�E�E�H�Ƃ�����������邽�߂Ɏg��ꂽ�̂��A���̂𐔂���Ƃ��̏����̏����ł���P�P�Ή��ł����B
����̈����̏��Ƃ́A���̂P�P�Ή����t�����p���Ă��܂��B�����Ɗ��������P�P�Ή������Ă��܂��B
���ʂ͐����Ɣ����Ǝv����������������ɐ����ƂP�P�Ή����Ă��܂��܂��B���̑��̐��̕��т��P�P�Ή����Ă��܂��܂��B��������������ł��B
���o�[�g�̂悤�ȏ��N�ɂ́A���o�I�ɏ펯�ƈقȂ鐢�E�����邱�Ƃ��点�邭�炢���ւ̎R�ł͂Ȃ������ł��傤���B
�����ŁA�s�v�c�Ɏv���A���w�ɋ����������ĕ����n�߂�Ƃ����̂��ǂ��q�̃X�g�[���[�Ȃ̂ł����A�Ȃɂ��A���̐��E�̃v���f���[�T�[�͈����Ȃ̂ł��̂悤�ȓW�J���҂��Ă���Ƃ͌���܂���B
���������������o�[�g���N�ɃI�X�X���̖{�́A�u�����_�̋����v�i���Ύ��F�u�k�Ќ���V��1998�N9��20���F\660�~�j�ł��B
���̖{�̃��r���[���̂��ʔ����̂ŁA�{�̏Љ�T�C�g�ɒ���y�[�W�̉��̕��ɍs���āA����ǂ�ł݂Ă��������B�{�̒l�i���A�������������Ƃ͈قȂ�l�i���t���Ă��܂����A���ꂾ�����Ԃ��o���Ă���Ƃ������Ƃł��B
----- �����܂� 20140720 -----
����P�O��
��Ђ̃}�W�b�N�Ƃ����\��Ȃ̂ŁA���Z�p�`����h�����āA�ǂ����ɓ�����Ă����̂��Ǝv������A�n�܂����̂̓t�B�{�i�b�`���ł����B
�t�B�{�i�b�`�����P�C�P�C�Q�C�R�C�T�C�W�C�P�R�C�Q�P�C�R�S�C�T�T�C�W�X�C�E�E�E
�P���@�P���P
�Q���@�P���Q
�R���@�Q���P�D�T
�T���@�R���P�D�U�U�U�U�U�U�U�U�U�E�E�E�@
�W���@�T���P�D�U
�P�R���@�W���P�D�U�Q�T
�Q�P���P�R���P�D�U�P�T�R�W�S�U�P�T�E�E�E
�R�S���Q�P���P�D�U�P�X�O�S�V�U�P�X�E�E�E
�T�T���R�S���P�D�U�P�V�U�S�V�O�T�X�E�E�E
�W�X���T�T���P�D�U�P�W�P�W�P�W�P�W�E�E�E
���̎������Ă����l�́A�ǂ�ȈӖ��������Ă���̂��낤�Ǝv���A�T���Ă݂�Ɓu�������v�Ƃ������Ƃ�������܂����B
�������̓��i�t�@�C�j�ŕ\����āA�ȉ��̎��ŕ\������܂��B
�����i�P�{��i�T�j�j�^�Q
����́A�Q���������@X^2�|X�|1��0�@�̐��̉��ɂȂ�܂��B
���̈����́A���̉������������Ȃ�A�����ŕ\���܂������A���ʂ̕����ł������ɂ��Ȃ�̂ɁA���w�Z�A���w�Z�A�����Ă���ȍ~�����ڂɂ����������Ƃ��Ȃ��A�������o�Ă��邱�ƂɈ�a���������܂��B
�����P�{�P�^�i�P�{�P�^�i�P�{�P�^�i�P�{�P�^�i�P�{�E�E�j�j�j�j
���ɁA�}�`���܊p�`��`���āA���̈�ӂ̒����ƁA���̐��܊p�`�̑Ίp���̒������r���܂��B
���܊p�`�̈�ӂ̒������P�Ƃ���ƁA���̑Ίp���̒����́A���ɂȂ�܂��B
���A��ӂ̒��������̐��܊p�`��`���āA���̑Ίp���̒��������Ƃ��܂��B
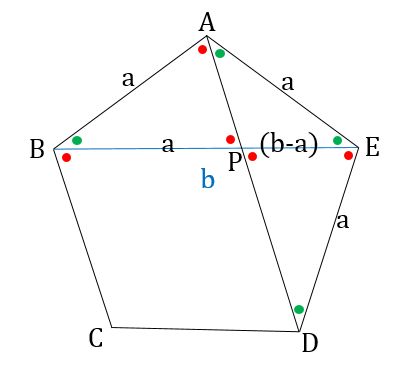
��ABE�䁢APE�ł�����A���F�����i���[���j�F���ƂȂ�܂��B
�@�@���i���|���j�����O2
�@�@���O2�[�����[���O2���O
�@�@�����P�@�ł�����
�@�@���O2�[���[�P���O
���̂Q���������̉��́A���i���������j�ł����B�߂ł����A���f�^�V�B
�����Ȃ�A�����͌܊p�`���\�����Ă�����A�_�A�ʂ̘b���n�߂܂����B���ꂼ��̐��̊W���ʔ����Ƃ����̂ł��B
�������A���̐����͌܊p�`�ɗ��܂炸�A�����镽�ʐ}�`�Ɉ�v���鐫���ŁA��Ɂu�P�v�ɊW�Â�����Ƃ����̂ł��B
����ɁA���ʐ}�`�ɂƂǂ܂炸�A���̊W�͗��̐}�`�ɂɂ������āA�u�Q�v�ɊW�t������Ƃ����̂ł��B
�����̊W���瓱���ꂽ�u�P�v��u�Q�v�̓I�C���[���ƌ����悤�ŁA���̐�ɂ͈ʑ��w�i�g�|���W�[�j�Ƃ������E���L�����Ă���悤�ł��B
----- �����܂� 20140727 -----
����P�P��
�ؖ��ł��B
�w���@�Ɛ��w�I�A�[�@���܂����ɕ����т܂��B�}�`�ł͕⏕���A���̕⏕�����������Ȃ��ĚX���Ă���p�������т܂��B
�ؖ��͘_���̊K�i���ЂƂÂo���Ă䂭�悤�Ȃ��̂ł��B
�L���ǂ���ł́A�t�F���}�[�̍ŏI�藝�ƃ|�A���J���\�z���ؖ�����A���[�}���\�z���܂��ؖ�����Ă��Ȃ��Ƃ����̂��ŋ߂̘b��ł����B
�t�F���}�[�̍ŏI�藝�͌`���P���Ȃ����ɁA�ŏ������u�Ԃ���A�u�����ؖ��ł���v�Ǝv���Ă��܂��̂ł����A���ǂR�O�O�N�ȏ�����w�҂�����Y�܂����̂ł����B
���w�ŐH�ׂĂ������Ǝv������A�����Ď���o���Ă͂Ȃ�Ȃ����̂������悤�ł��B���̏ؖ��̂��߂ɁA�Ⴍ�č˔\�̂��鐔�w�҂̗��������A���l���ׂ�Ă������悤�ł����A�܂����𐬂����吔�w�҂̍˔\�������D���Ă����������ł����B
������A���w�E�ł̓t�F���}�[�̍ŏI�藝�Ɏ��g��ł���Ƃ������Ƃ͂������҂�ɂ͌����Ȃ��āA�t�c�[�ɐ��w�҂����Ă��Ȃ���e�ŏؖ��Ɏ��g��ōs���Ȃ��Ă͂Ȃ�܂���ł����B
�C�M���X�̃��C���Y���͂V�N�ԁA�ЂƂ�Ńt�F���}�[�Ɗi�����Ă��܂������A�P�X�X�S�N�ɏؖ����܂����B�_���͂Q�O�O�y�[�W�ȏ�B���ǂ������w�҂��^�ɒl���܂��B�t�F���}�[�E���C���Y�̒藝�ƂȂ��āA���j�ɍ��܂�܂����B
���̒藝�Ɏc���ꂽ���Ƃ����A�u�����I�Ɂv�������ƁB�����邱�Ƃ͕�����܂������A���㐔�w�̂����鐬�ʂ��Ă���ɂ����悤�ȂQ�O�O�y�[�W�̘_���ł͂Ȃ��āA�t�F���}�[�̏��L���Ă������w���̗]���ɏ������߂���x�̏ؖ����c����Ă���̂ł��B
�|�A���J���\�z�́A�ʑ��i�g�|���W�[�j���g���ďؖ��ł���ƍl�����Ă��܂������A���V�A�̃y�����}�������u�����v�̎�@���g���ďؖ������悤�Ȃ̂ł��B�u�悤�ȁv�Ƃ��������悤�̂Ȃ��A�܂������ł����킩��Ȃ�����̐��E�ł�����B
���A�e���r�I�ɗL���ǂ���̖��������Ƃ��ẮA���[�}���\�z�͂��ؖ������̂��A�y���݂ł��ˁB
���ŏ��Ɏv�������w���@���݂Ă݂܂��傤�B
�y�f���������ɂ��邱�Ƃ̏ؖ��z
�f�����L�������Ȃ��Ɖ��肷��B
���̌������Ƃ��C���ׂĂ̑f�������������ɂȂ�ׁC
�������o1�C�o2�C�o3�C�o4�C�o5�C�E�E�E�C�on�Ƃ���B
�i�o���͍ő�̑f���ł���E�E�E�@�j
���̂Ƃ��C�p�� �o1�~�o2�~�o3�~�o4�~�o5�~�E�E�E�~�on �{�P�Ƃ������p���l����B
����ƁC�p�̌`���C�p�͑f���ł���E�E�E�ǂ̑f���i�o1�C�o2�C�o3�C�o4�C�o5�C�E�E�E�C�on�j�ł���Ă��P���܂邩��B
�܂��C�@���C�p�͑f���ł͂Ȃ��E�E�E�ő�̑f�����傫������B
����āC�����B
���������āC�͂��߂̉��肪���ł��������ƂɂȂ�C�f���͖����ɂ���B
�����ɐ��w�I�A�[�@�ɂ��Ă݂Ă݂܂��B
n�Ck�����R���Aa�Cb���O�ȏ�̐����Ƃ���ƁA
����o(n)�F�U^n���P�O�a�{�U�ł���B
n���P�̂Ƃ�
�U^1���P�O�~�O�{�U
����āA�o(1)�͐��藧�B
n��k�̂Ƃ��A�o(k)�����藧�Ƃ���ƁA
�U^k���U�b�{�U
���̂Ƃ��o(k�{�P)��
�U^(k+1)���i�P�O����{�U�j�~�U
�@�@�@�@���U�O�b�{�R�U
�@�@�@�@���P�O�~�i�U�b�{�R�j�{�U
����Ăo(k�{�P)�����藧�B
�ȏォ��A���ׂĂ̂��ɂ��Ė���o(n)�͐��藧�B
�Ƃ���ŁA�C���h�̃��}�k�W�������ɂƂ��ďؖ��͂���قǕK�v�ɂ͌����Ȃ��悤�ł��B�����ŎR�قǂ̒藝��������ł���悤�Ɍ�����̂ł��B
�������A�ؖ��Ȃ����āA���҂ɂ��̐������𗝉������邱�Ƃ͍���ł��B���w�Őg�𗧂Ă�Ƃ��ϓ_���猩��A�ނ͕s���̂����ɎႭ���ĕa�����܂����B
����ł��A�����̓��Ȃ鐺��\�����邱�Ƃ��ł������ƁA�ނ̐��w�I�����𗝉����āA�ނ̒藝���ؖ����Ă������C�M���X�̐��w�҃n�[�f�B���Ƃ��������҂ɏ��������Ƃ��l����ƁA�ĊO�K���������̂�������܂���B
----- �����܂� 20140801 -----
����P�Q��
����̖��ɓo�ꂳ��鐔�w�҂́A���b�Z�����A�N���C�����A�J���g�[�����A�I�C���[���A�K�E�X���A�s�^�S���X���A�t�B�{�i�b�`���A�����Ė��O�͓`����Ă��Ȃ�����ǐl�Ԃ��������Ă��琔�w�Ƃ������E��z���グ�Ă������E�̐l�X�B
���{�̊֍F�a���̂��p�������܂���ł������H
�܂��Ȃ������̓��o�[�g�ƕ�����Ď����̌����ɖ߂�܂��B�ǂ�Ȍ��������Ă���̂��͖����������܂��ł����B�ĊO�A���[�}���\�z�Ɏ��g��ł���̂�������܂���B
���o�[�g�͖�����o�߂Ă��A�����������������̌M�͂��茳�ɂ���̂ɋC�Â��܂��B�����̐�����Z�Ƃ����Ƃ���ł��B���o�[�g�̂��ꂩ���\��������ł��ˁB�����̐��Ȃ͂��炢�Ƃ����̂ł��傤���B
�P�Q�邪�߂��āA��������o�߂Ă݂�ƁA�Z���E���w���y�����Ȃ��Ă��܂����B
��P�P��ŁA���b�Z�������P�{�P���Q���ؖ�����A�Ƃ������i������j������̂ł����A�P�{�P���Q�Ƃ͂��������ؖ����邱�ƂȂ�Ă��蓾��̂��낤���Ǝv���̂ł����B
�Ƃ��낪�A�^�����Ɏv�l����Ƃ����ł͂Ȃ��炵���B�ł��A�ؖ�����ɂ́A�܂��W���Ǝʑ��𗝉����Ă��Ȃ��Ǝn�܂�Ȃ��悤�ł��B�����ďؖ��̓�������ɁuPeano�̌����v������āA����𗊂�ɑ����̂��Ƃ��`���āA�����Ă��̒�`���ؖ����āE�E�E���J��Ԃ��āA�Ō�̍Ō�ɂP�{�P���Q�͏ؖ������悤�ł��B
������˂��l�߂Ă����ƍ������̍�������T���Ă���悤�Ȋ��������āA�������A������O�Ǝv���Ă������Ƃ��炪�����玟�ւƂ���ӂȐ��E�ɕ��荞�܂�čs���̂ł��B
�u�܁A�������v�œ�����߂����Ă��Ă��A���������ɐ����Ă�����̂ł����A�u�ǂ����āH�v��{�C�ōl���n�߂�ƁA����Q���Ȃ��Ȃ�܂��B���X���������O�ɁA���ɐ�l�������l���Ă���Ă������ƂׂāA�����ė������邱�Ƃ��ł���A���̓��͈��S���Ė��邱�Ƃ��ł��܂��B
�N���܂�������Ă��Ȃ��������̖��Ɏ��g��ł��鐔�w�҂̂��Ƃ�z������ƁA���ߑ����o�Ă��܂��܂��B
���������A�L���Ȗ�������肪����܂��B
�u�N���C���w��������2000�N�ɐ��w���7�̖���������1���~�̌��܋���������Ɣ��\���܂����B
���̂����́u�|�A���J���\�z�v��2�N��Ƀ��V�A�̐��w�҃O���S���[�E�y�����}���ɂ���ďؖ�����܂������A14�N�����������Ȃ��c���6�͉�����Ă��܂���B�v
�V������������܂����A��莩�̂����������Ă���̂������ł��Ȃ��̂��A�߂����ł��ˁB
���@�@�@�@�@���@�@�@�@�@���@�@�@�@�@��
�P�A����-�~���Y�������̑��݂Ǝ��ʃM���b�v���
�u�C�ӂ̃R���p�N�g�ŒP���ȃQ�[�W�Q G �ɑ��� R^4 ��̎����łȂ�����-�~���Y��̗ʎq�_�����݂��A���ʃM���b�v�����݂��邱�Ƃ������邩�H�v
�����E�~���Y�������̑��݂Ǝ��ʃM���b�v���Ƃ́A�C�ӂ̃R���p�N�g�ȒP���Q�[�W�Q G �ɑ��āA���ȗʎq�����E�~���Y���_�� R^4 ��ɑ��݂��A���ʃM���b�v �� > 0 �������Ƃ��ؖ�����A�Ƃ������ł���B���݂Ƃ́AStreater & Wightman (1964)�AOsterwalder & Schrader (1973) �� Osterwalder & Schrader (1975) �Ɏ咣����Ă��邱�ƂƏ��Ȃ��Ƃ������Ȋm�����ꂽ�����I�Ȑ����������Ƃ��Ӗ����Ă���B
���p�Fwikipedia
�Q�A���[�}���\�z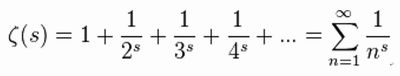
��(s) �̎����łȂ���_ s �́A�S�Ď�����1/2�̒�����ɑ��݂���̂��H
�ŋ߂ł́A������������������10���� (X. Gourdon and P. Demichel, 2004) �܂ł̕��f��_�͑S�ă��[�}���\�z�������Ƃ��v�Z����Ă���A���݂܂łɂ܂�����͒m���Ă��Ȃ��B���݂ł͑����̐��w�҂��i���R�̂��Ƃ����A�͂����肵���������������Ɂj���[�}���\�z�͐������ƍl���Ă���悤�ł���B
�����������ɂ����_���猩����������L���̐��\�Ȃǂ͗�_���z�̑S�e�𖾂炩�ɂ���ɂ͎���Ȃ��Ƃ��āA���̐��l�v�Z�̌��ʂɑ��ĐT�d�Ȑ��w�҂�����B���j��L���Ȑ��w�҂̒��ł����[�}���\�z���^���Ă������w�҂͂���B
���p�Fwikipedia
�R�AP��NP�\�z
�N���XP�ƃN���XNP�͓������Ȃ��̂��H
�N���XP�Ƃ́A���萫�`���[�����O�@�B�ɂ����āA���������ԂŔ���\�Ȗ��̃N���X�ł���A�N���XNP�́AYes�ƂȂ�؋��iWitness�Ƃ����j���^����ꂽ�Ƃ��A���������Ԃ�Witness�̐������̔���i��������Ƃ����j���\�Ȗ��̃N���X�ł���B
���������ԂŔ���\�Ȗ��́A���������ԂŌ��؉\�ł���̂ŁAP��NP�ł��邱�Ƃ͖��炩�ł��邪�AP��NP�̐^�����W���ł��邩�ۂ��ɂ��Ă͖��m�ł͂Ȃ��B
�ؖ��͂܂��������A�����̌����҂�P��NP���ƐM���Ă���B�����āA���̃N���XP�ƃN���XNP���������Ȃ��Ƃ����\�z���uP��NP�\�z�v�Ƃ����B
���p�Fwikipedia
�S�A�i�r�G-�X�g�[�N�X�������̉��̑��݂Ɗ��炩��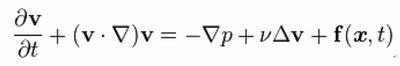
�i�r�G-�X�g�[�N�X�������̉��̊�{�I���������A�ؖ�����Ă��Ȃ��B
�������� 3�����̌n�ɂ��ď����������^����ꂽ�Ƃ��A���炩�ȉ�����ɑ��݂��邱�ƁA�������݂���Ƃ����炻�̉������ʓ�����L�E�ȃG�l���M�[�������Ă��邩�Ƃ������Ƃ��A���w�I�ɂ͂��܂��ɏؖ�����Ă��Ȃ��B���̖����̉��̑��݂Ɗ��炩���̖��Ƃ����B
���p�Fwikipedia
�T�A�z�b�W�\�z
���f��͑��l�̂̂���z�����W�[�ށi�z�b�W�ށj�́A�㐔�I�ȃh�E���[���R�z�����W�[�ނł��낤�A�܂�A�������l�̂̃z�����W�[�ނ̃|�A���J���o�̘a�Ƃ��ĕ\�����悤�ȃh�E���[���R�z�����W�[�ނł��낤�Ƃ����\�z�B
���p�Fwikipedia
�U�A�|�A���J���\�z�i�����ρj
�P�A����3�������l�̂�3�������� S^3 �ɓ����Ȃ̂��낤���H
2002�N����2003�N�ɂ����ē����X�e�N���t���w�������ɋΖ����Ă������V�A�l���w�҃O���S���[�E�y�����}���̓|�A���J���\�z���ؖ������Ǝ咣���A�_�����v���v�����g���e�T�C�g�Ƃ��Ē�����arXiv�ɂČ��\�����B
���̂Ȃ��Ŕނ̓��`���[�h�E�X�g���C�g�E�n�~���g�����n�n�������b�`�t���[�iRicci flow�j�̗��_�Ɂu��p�v�ƌĂԐV���Ȏ�@��t�������Ċg�����A�����ׂ����ƂɃT�[�X�g���̊��\�z���������Ă��̌n�Ƃ��ă|�A���J���\�z�����������i�Ɛ錾�����j�B
���ɒP���Ɍ����A���\�z�Ƃ́A���l�̂�8�̃s�[�X�ɕ������A���̃s�[�X���ɊI�����ׂ�Ƃ������̂ł���B����ŁA���b�`�t���[��p�����Ƃ��ɁA�s�[�X����S�̂��\���������Ƃ��ɓ��ٓ_����������\��������B
�y�����}���͂��̓��ٓ_�̔��������Ɠ��ٓ_�̐����ׁA���ٓ_���������Ȃ��悤�Ȏ�@���l�����B���ꂪ�u��p�v�Ƃ�������@�ł���B
�قƂ�ǂ̐��w�҂��g�|���W�[���g���ă|�A���J���\�z���������Ƃ����̂ɑ��A�y�����}���͔����w�ƕ����w�̎�@���g���ĉ����Ă݂����B
���̂��߁A���̐��������߂��ăA�����J�̒d��ɗ������y�����}���̉���������w�҂����́A�u�܂��A�|�A���J���\�z�������ꂽ���Ƃɗ��_���A���ꂪ�g�|���W�[�ł͂Ȃ������w���g���ĉ����ꂽ���Ƃɗ��_���A�����āA���̉��̉�����܂����������ł��Ȃ����Ƃɗ��_�����v�Ƃ����B
���p�Fwikipedia,msp.warwick.ac.uk
�V�A�o�[�`�E�X�E�B���i�[�g�����_�C�A�[�\�z
�ȉ~�Ȑ�E��̗L���_�Ɩ������_O�̂Ȃ��L�������A�[�x���Q�̊K���i�����N�j���AE��L�� L(E, s) ��s=1�ɂ������_�̈ʐ��ƈ�v����̂��H
���@�@�@�@�@���@�@�@�@�@���@�@�@�@�@���@�@�@�@�@��
�����Ɂ@�u������Ȃ��v�@�Ɣ���Ƃ��납��A�������n�܂�ƐM�������̂ł��B
�����ɓ��B���邽�߂ɂ́A�[��������n�߂Ȃ���Ȃ�܂��A�[�Ō������Y��ȏ����E���Ċ��������Ă���A�Ƃ����̂�����ł��B����ł��\���y�����āA�K���ł��B
----- �����܂� 20140806 -----