負×負=正 update20081103
負×負=正(1)
式だけ追跡していくだけでも、 負×負=正 を見いだすことはできるのです。
a、b>0なる任意の実数a、bにおいて
a×0=0
のとき
a=2×a+(−a)
0=b+(−b)
とおくと
〔2×a+(−a)〕×〔b+(−b)〕=0
である
∴ 2×a×b+2×a×(−b)
+ (−a)×b + (−a)×(−b)=0
2×a×b+2×a×(−b)=0であるから
(−a)×b+(−a)×(−b)=0
両辺に a×b を足すと
(−a)×(−b)= a×b
したがって 負×負=正 であることが示されました。
しかし、式の変形では、腑に落ちない。
なんとなく、まやかしにあったような気がするのではないのでしょうか。
「借金 × 借金 = 貯蓄」
になるような感覚をうち破る、
感覚的な説明が必要な気がするのです。
----- ここまで 20081101 -----
負×負=正(2)
符号(+,−)の意味を考えています。
1 基準からの増減
2 方向の反転
3 意味の反転
いろいろな例を思い出してみて、思いつくままに意味を考えてみました。
上の3つでも、意味が重複しているぞ、と言われるかもしれませんし、
まだこんな意味がある、ということもあるでしょう。
足りない能力は許してもらって、
着目したいのは3番目の「意味を反転する」符号というところです。
具体的に記述してみます。
(+1) × (+ 3) = +3
山がひとつ (そのままの意味で)その3倍 山が3つ
(+1) × (− 3) = −3
山がひとつ(反対の意味にして)その3倍 (山の反対の)穴が3つ
(−1) × (+ 3) = −3
穴がひとつ (そのままの意味で)その3倍 穴が3つ
(−1) × (− 3) = +3
穴がひとつ(反対の意味にして)その3倍 (穴の反対の)山が3つ
直感的に分かるでしょうか。
----- ここまで 20081102 -----
負×負=正(3)
ちなみに、「やりなおし基礎数学:小野田襄二著」では、
「第6章 負の数のかけ算はプラスか?」と、
1章をさいて記述しています。
最終的には、「プラスとマイナスの平面座標への発展」
という項目に発展させて、理解するように記述されています。
一方、「算数・数学が得意になる本:芳沢光雄著」では、
「第2部中学編 2−2 【負の数】を含む掛け算・割り算」と、
やはり1章をさいて記述しています。
この本の特徴は、
「乗除でつまずく者は、加減でつまずいていないか。」という問いを発し、
分からない子にはそこから丁寧に説明してやらなければ、
乗除は分からないとして、本当に丁寧に、
マイナスを含む加減の説明をしていることです。
芳沢氏は、多くの中学の先生と話し合ったところ、
「マイナス×マイナスがプラス」になることを理解させる
いくつかの方法があるうちで、最適なのは、
「 速さ × 時間 = 距離 」
を用いることである、というのだそうです。
速さ=(単位時間に進む距離)と(進んだ方向【右か左、東か西】)
時間=(かかった時間)と(時間の方向【→未来か過去か】)
速さにも時間にも、単なる量のみではなくて、
進むのか(or)戻るのか、何分後なのか(or)何分前なのか、
方向の反転の意味を符号にもたせていることが分かります。
たとえば、太郎君の現在の地点(移動する距離の起点であり、
計測する時間の起点でもある)から、
・東を進む方向のプラスの向きとして
・何分後(未来)を時間の方向のプラスとする
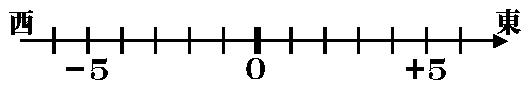
と、次のようなことが、考えられます。
太郎が毎分50mで歩くとすると
・東の方向に歩いているとき、60分後の太郎君の移動距離
この場合、(東→プラス)、(後→プラス)ですから、
(+50)×(+60)で表せます。
答えは、東へ3000mのところだから、
(+50)×(+60)=(+3000)
・西の方向に歩いているとき、60分後の太郎君の移動距離
この場合、(西→マイナス)、(後→プラス)で、
答えは西へ3000mのところだから、
(−50)×(+60)=(−3000)
・東の方向に歩いているとき、60分前に太郎君がいたところ
この場合、(東→プラス)、(前→マイナス)で、
答えは西に3000mのところだから、
(+50)×(−60)=(−3000)
・西の方向に歩いているとき、60分前の太郎君がいたところ
この場合、(西→マイナス)、(前→マイナス)で、
答えは東に3000mのところだから、
(−50)×(−60)=(+3000)
非常にイメージしやすい説明の要領だと思います。
「マイナスの数」ではなく、「マイナスの符号の意味」を理解すること、
これが重要だと思いました。
----- ここまで 20081103 -----