嶰暯曽偺掕棟丂update 20101209
嶰暯曽偺掕棟
捈妏嶰妏宍偺嶰暯曽偺掕棟偵偮偄偰徹柧傪帋傒傑偡丅
暿柤乽僺僞僑儔僗偺掕棟乿偼桳柤偱丄徹柧偺曽朄偼壗庬椶偐偁傞偼偢側偺偱偡偑丄乽傆乣傫乿偲姶怱偟偰偼偄偨傕偺偺丄帺暘偱夝偄偨帠偑堦搙傕偁傝傑偣傫偱偟偨丅
偦偙偱丄偙傟傪婡夛偵丄嶲峫彂傗嫵壢彂傪嶲峫偵偣偢丄恾偲偵傜傔偭偙偟偰丄側傫偲偐徹柧傪偟偰傒傛偆偲巚偭偨偺偱偡丅
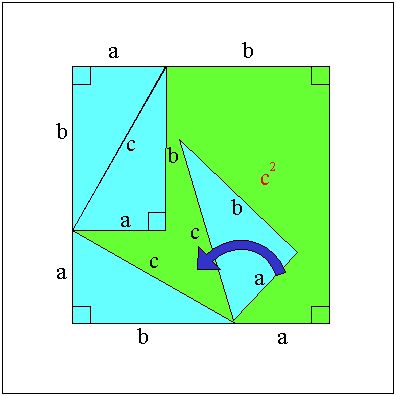
徹柧偵巊偆捈妏嶰妏宍偼丄忋偵偁傞傛偆側傕偺偱偡丅
傑偢巚偄偮偄偨偺偼丄嶰妏宍偺憡帡傪巊偆偙偲偱偡丅
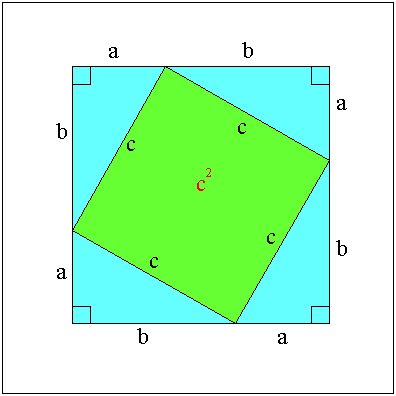
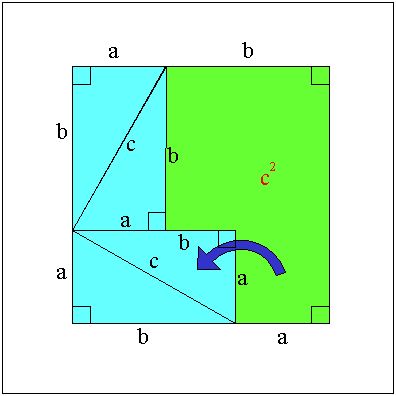
丂乮徹柧偦偺侾乯
丂仮俙俠俛偼捈妏嶰妏宍偱偁傞丅
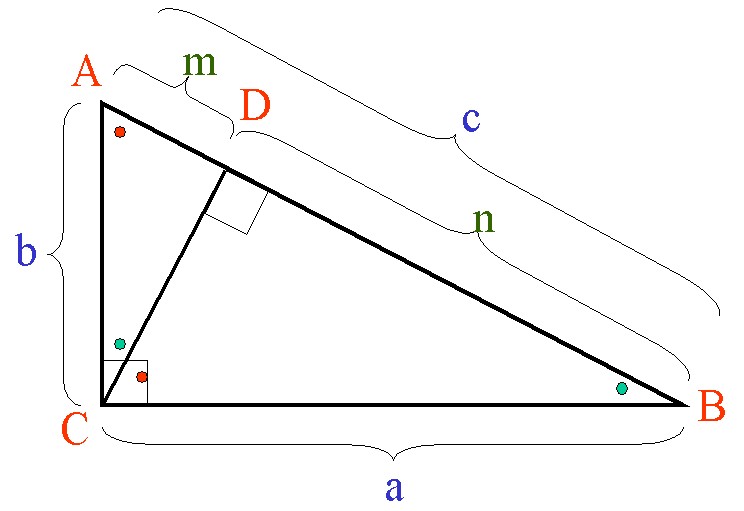
丂 佢俠亖佢俼偺捀揰俠傛傝丂幬曈們偵悅慄傪崀傠偟
丂幬曈偲偺岲揮傪俢偲偡傞丅丂偙偺偲偒幬曈俠偼揰俢偵傛傝
丂値偍傛傃倣偵暘妱偝傟傞丅
丂偙偙偱丄仮俛俙俠佷仮俛俠俢佷仮俠俙俢偱偁傞丅
丂偟偨偑偭偰奺嶰妏宍偵偍偗傞奺曈偺斾偼摍偟偄偺偱
丂値丗倎 亖 倎丗們丂丒丒丒丒嘆
丂倣丗倐 亖 倐丗們丂丒丒丒丒嘇
丂傑偨丂倣亄値 亖 們丂丒丒丒丒嘊丂偱偁傞偐傜
丂嘆傛傝
丂値乛倎 亖 倎乛們丂丂仺丂丂値 亖 倎^2乛們丂丒丒丒丒嘋
丂嘇傛傝
丂倣乛倐 亖 倐乛們丂丂仺丂丂倣 亖 倐^2乛們丂丒丒丒丒嘍
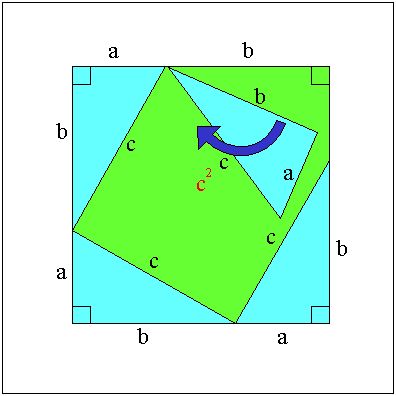
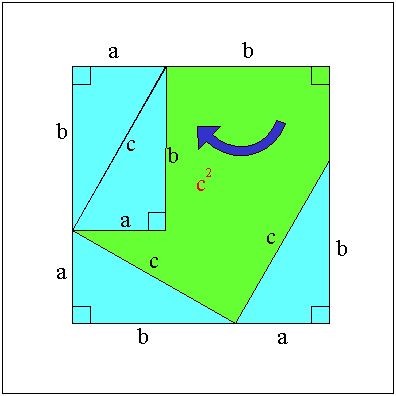
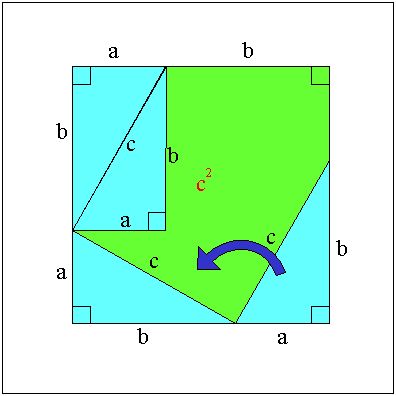
丂嘊嘋偍傛傃嘍傛傝
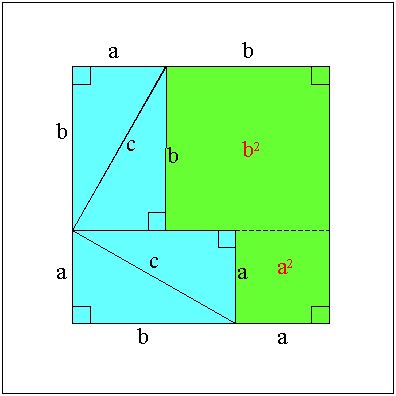
丂倣亄値 亖 倎^2乛們 亄 倐^2乛們
丂丂丂丂們 亖 倎^2乛們 亄 倐^2乛們
丂偙偺椉曈偵們 乮亗 侽乯傪忔偢傞偲
丂倎^2 亄 倐^2 亖 們^2
丂嶰暯曽偺掕棟偵側傝傑偟偨丅丂徹柧廔傢傝傑偟偨丅乮偮偯偔丒丒丒偐側乯
----- 偙偙傑偱丂20090910 -----